Теоретическое определение параметров процесса резания ширина и толщина среза при несвободном резании. Теоретический метод определения обрабатываемости материалов резанием, страница 46

4) в логарифмических координатах  (рис   54)  строится зависимость v₀₌f(a₁)  и находится формула вида  (280). Второй метод можно использовать и без измерения температуры резания, когда это затруднительно. Встречаются пары резец —- деталь, когда при широком изменении v и температуры резания значение термоэлектродвижущей силы при использовании естественной термопары очень мало (до 0,5 милливольта), изменяется направление термотока  (полярность)  при незначительном росте температуры резания. Такие случаи наблюдаются иногда при обработке жаропрочных   сталей   и   сплавов , резцами из различных быстрорежущих сталей. Оба метода экспериментального определения обрабатываести не требуют проведения опытов по износу инструмента и дают практически совпадающие результаты в виде степенных формул (280).

Значения постоянных величин с_v и у, входящих в формулy (280), для 37 пар обрабатываемый материал — инструментальный материал приведены в табл. 27.

С учетом формулы (280) можно получить следующие упрощённые выражения: для   оптимального   относительного   поверхностного   износа

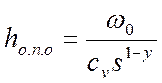        (282)

где 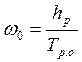 — оптимальная скорость износа; для максимальной размерной стойкости инструмента

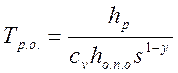         (283)

ОПРЕДЕЛЕНИЕ ОПТИМАЛЬНЫХ РЕЖИМОВ РЕЗАНИЯ ЦВЕТНЫХ СПЛАВОВ НА СТАНКАХ С ЧПУ

Широкое внедрение в промышленность станков с программным управлением вызвало необходимость определения оптимальных режимов резания на них с учетом точности обработки, жёсткости технологической системы СПИД и шероховатости обработанной поверхности Ниже излагаются результаты исследований по определению оптимальных режимов резания при обработке цветных сплавов на токарных и фрезерных станках с программным управлением [35]. Исследовались цветные сплавы на медной, алюминиевой и магниевой основах (табл. 28).

Обработка на токарных станках. При точении эксперименты проводились на токарном станке с программным управлением модели 1А616ФЗ. Обрабатывались сплавы на алюминиевой основе: Ал2, Ал9, В95, Д16Т и АМЦ-50, сплавы на основе магния Мл5 и Мл2-1 и медные сплавы Л62 и ЛС59-1. Инструментальный материал ВК6. Геометрия инструмента: α=10⁰; γ= 10° + 22⁰; φ = 45°; φ₁ = 10°; r = 0,5÷1*10^-3 м.

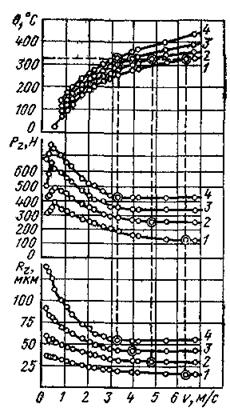Рис. 55. Температурно-силовые   зависимости  и  изменение  высоты неровностей  при обработке точением сплава Ал9 резцом из сплава ВК6: 1-s=0,11 • 10^-3 м; 2-s=0,195 • 10^-3 м; 3-s=0,3 • 10^-3 м; 4-s=0,43 • 10^-3 м; t=1 • 10^-3 м; φ=45°; φ₁=10^o ; γ=10°;  α=10°; r=l • 10^-3 м:

В процессе исследований при широком изменении диапазона скоростей резания и подач производились замеры температур и сил резания. По результатам исследований для всех материалов строились температурно-силовые зависимости, критериальная зависимость Pe=f(A), а также график зависимости минимально-стабилизированного значения силы резания от подачи. В качестве примерз темпе-ратурно-силовые зависимости при обработке сплава Ал9 приведены на рис. 55.

После подстановки конкретных  числовых значений всех величин в формулу (272) получали формулу для оптимальной скорости резания в виде

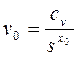                            (284)

где с_v и x₀ — числовые величины, определяемые из табл. 29.

Значение подачи s, подставляемое в формулу (284), целесообразно определять с учетом точности обработки и жесткости технологической системы. При обработке цилиндрических деталей из исследуемых материалов на станке 1А616ФЗ получены следующие теоретические формулы для определения подачи по допустимой точности обработки;

при обработке деталей в центрах с вращающимся задним центром

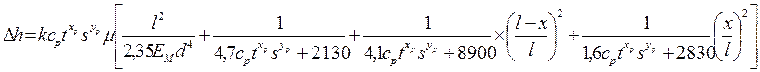(285)