Теоретическое определение параметров процесса резания ширина и толщина среза при несвободном резании. Теоретический метод определения обрабатываемости материалов резанием, страница 27

Величина АВ связана также с радиальным износом:

Приравнивая выражения для АВ, получим

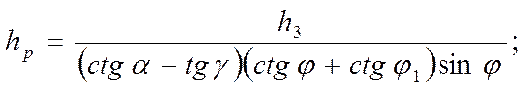(229)

Таким образом, теоретическая взаимосвязь между h_з и h_з определяется углами резца α, γ, φ и φ₁ Формула  (229)  справедлива для резцов с радиусом при вершине, равным r=0;

ТЕОРЕТИЧЕСКОЕ   ОПРЕДЕЛЕНИЕ   ВЫСОТЫ   НЕРОВНОСТЕЙ В УСЛОВИЯХ ОПТИМАЛЬНОГО РЕЗАНИЯ

Теоретическое определение высоты неровностей необходимо для решения задачи об ограничении выбора подачи «сходя из заданной операционным эскизом технологического процесса шероховатости обработанной поверхности. Экспериментально доказано [13, 29], что на величину высоты неровностей R_z и , среднее арифметическое отклонение профиля R_a влияют не только геометрия инструмента (φ, φ₁, r и т.д.) и режимы резания (v, s, t), но и пластические деформации металла в поверхностном слое летали. Поэтому очень часто фактическая высота неровностей  R_z превышает их расчетные значения, определяемые из чисто геометрических соображений. Однако опыты показывают [51], что при обработке большого количества цветных сплавов, легированных и нержавеющих сталей, а также жаропрочных и титановых сплавов в условиях резания с оптимальными температурами пластические деформации вызывают незначительное изменение высоты неровностей  R_z

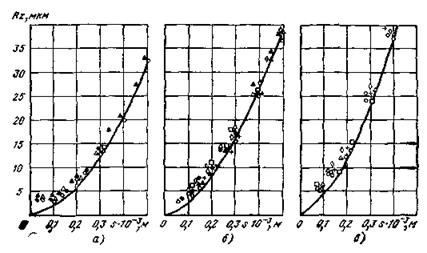
Рис. 40. Сопоставление расчетных значений Кг 

(сплошная линия)  со значениями, полученными экспериментальным путем  с использованием оптимальных режимов  резания   (опытные данные получены В. А. Козловым и др. под руководством   В. Ф. Безъязычного) (рис. 40). Поэтому для условий оптимального резания открывается возможность приближенного расчета подач, исходя из требуемой шероховатости, по известным теоретическим формулам следующего вида:

для точения резцами с r=0, а также для сверления, зенкерования, развертывания и торцового фрезерования

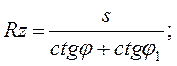
для точения резцами с r≠0 и цилиндрического фрезерования с r=R  (R -  радиус фрезы)      

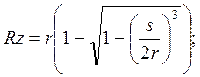
Решая относительно подачи s, получим;

  (230)

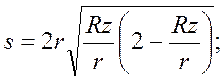    (231)

Заметим, что при обработке, многолезвийным инструментом, ; как и при обработке резцом, определяется расчетом оборотная i подача s, так как в большинстве случаев технические условия , на изготовление новых инструментов допускают биение зубьев, превышающее. Следовательно, приближенно можно принять I положение о том, что шероховатость обрабатываемой поверхности преимущественно формируется одним наиболее выступающим зубом. Формулы  (230) и (231) включают в себя высоту i неровностей   по   ГОСТ  2789—73.   Если   в  операционной   карте технологического процесса требуемая шероховатость указана в виде среднего  арифметического    отклонения    профиля Ra, то можно пользоваться приближенным выражением  [51]

 (232)

Формула (231) может 'быть представлена в следующем известном приближенном виде:   Если в эту формулу подставить значение подачи s, найденное из теоретического уравнения (192), то высота неровностей Rz окажется связанной функционально с большим количеством технологических и физических параметров:

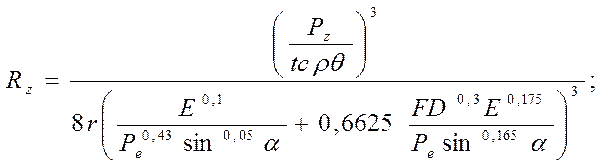(233)

Формула (233) показывает, что высота неровностей зависит не только от параметров, известных до опыта (Pe, F, D, E, r, α, t, cp), но и отношения параметров процесса резания Rz/θ. Для оптимальных условий резания в формулу (233) необходимо подставлять   значение Pz_min, определяемое   выражением (201), θ₀ и υ₀ в критерий Ре. Подобного рода формулы приведены и подробно проанализированы в работе [4].

ТЕОРЕТИЧЕСКАЯ ВЗАИМОСВЯЗЬ ОСТАТОЧНЫХ НАПРЯЖЕНИИ С РЕЖИМАМИ МЕХАНИЧЕСКОЙ ОБРАБОТКИ

Перед специалистами в области технологии машиностроения стоят большие задачи не только по дальнейшему увеличению производительности труда, получению деталей заданной геометрической формы и точности ее размеров, снижению себестоимости обработки, но и приданию деталям благоприятных эксплуатационных свойств по надежности и долговечности.