В заключение отметим, что если процессы резания характеризуются критериальной зависимостью в виде ломаной линии с двумя прямолинейными отрезками, то для определения оптимальных режимов резания необходимо принимать значения с1 и n, соответствующие второму прямолинейному отрезку, так как; последние обычно располагаются именно в этом интервале значений критериев А и Ре.
НОВЫЙ ЭКСПЕРИМЕНТАЛЬНЫЙ МЕТОД ОПРЕДЕЛЕНИЯ ОБРАБАТЫВАЕМОСТИ СТАЛЕЙ И СПЛАВОВ
Оптимальные условия резания, которым соответствуют максимальная размерная стойкость инструмента и наиболее благоприятные параметры точности и качества поверхностного слоя, наступают в момент стабилизации тангенциальной составляющей силы резания Pz=f(v), когда сохраняются постоянными t и s и геометрия инструмента. Многочисленные исследования позволили установить также [40, 41, 45], что моментом стабилизации функций Pz=f(v) при различных подачах s соответствует одно и то же значение оптимальной температуры резания θ0. Это позволяет предложить два новых экспериментальных метода определения обрабатываемости.
Первый экспериментальный метод определения обрабатываемости основан на критериальных зависимостях и состоит в следующем:
1) при каком-либо выбранном постоянном значении глубины резания t и постоянном значении s проводится несколько опытов с одновременным измерением Рz и θ при широком диапазоне изменения скорости резания v, включающем в себя скорость резания, при котором наступают Рzmin и оптимальная темпера тура θ0;
2) устанавливается критериальная зависимость вида (271) и уравнение скорости резания (272);
3) проводится 4—5 опытов при ранее выбранной глубине резания t(b1), различных подачах s(a1) и постоянной температуре θ0, причем постоянство температуры поддерживается путем соответствующего изменения скорости резания v0. В опытах измеряется тангенциальная составляющая силы резания Рzmin, для которой находится формула
![]() (279)
(279)
4) в формулу (272) подставляются числовые значения величин с1, а, b1, ср, θ0 и формула (279) и находится выражение вида
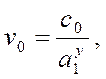 (280)
(280)
где у=1 — (1—х)n; x = 0,7÷0,9; n=1,5÷2,5 (для различных пар резец — деталь).
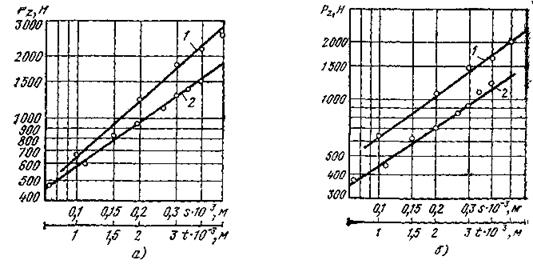 |
Рис. 50. Зависимость минимальной силы Pz от t и s:
s — при обработке сплава ХН56ВМКЮ резцами из Р9К10Ф: б — при обработке сплава ХН73МБТЮ резцами иа ВК6М: 1 - t; 2 - s
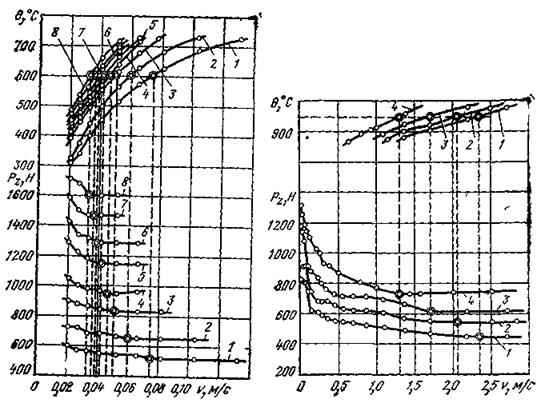 |
Рис. 51. Температурно-силовые зависимости при обработке сплава ХН56ВМКЮ резцами из стали Р18:
v=0,02÷0,132 м/с; s=0,074÷0,39•10-3 м; t=1 • 10-3 м; φ=45°; φ1 =45°; γ=12°; α=12°; 1-s=074 • 10-3 м; 2 -s=0,11 • 10-3 м; 3 — s=0,15 • 10-3 м; 4 — s=0,195 • 10-3 м; 5- s=0,26 • 10-3 м; 6-s=0,30 • 10-3 м; 7-s=0,34 • 10-3 м; 8-s=0,39 • 10-3 м
Рис. 52. Температурно-силовые зависимости при обработке стали ХН30ВМТ резцами из сплава ВК8:
(v=0.014÷2,72 м/с; t=1 • 10-3 м; φ=45°; φ1=45o ; γ=12°; α=12°; r=l • 10-3 м):
1-s=0,15 • 10-3 м; 2-s=0,195 • 10-3 м; 3-s=0,26 • 10-3 м; 4-s=0,34 • 10-3 м;
Типовые экспериментальные зависимости тангенциальной составляющей силы резания Pzmin от t и s приведены на рис.50
Экспериментальные формулы для тангенциальной составляющей силы резания Pzmin находились в виде:
![]() (281)
(281)
где cpz ,x0 и x-числовые величины , определяемые для некоторых марок обрабатываемых и инструментальных материалов по табл.26
Второй экспериментальный метод ,основанный на стабилизации сил резания, состоит в следующем :
1) при различных 5-6 значениях подач s(a1) , изменяющихся от верхнего предела к нижнему, и постоянной глубине резания t(b1) проводятся серии опытов с одновременным измерением тангенциальной составляющей силы резания Pz и температуры резания θ ( каждому значению подачи s соответствует своя серия опытов с широким бесступенчатым изменением скорости резания v от нижнего ее значения к верхнему с периодическим измерением Pz и θ)
2) строятся графические зависимости Pz=f(v) и θ=f(v) в обычной системе координат для всех значений s (рис.51,52,53)
Таблица 26
Значения величин ![]() ,x0,x для определения силы
,x0,x для определения силы ![]()
![]()
![]()
![]()
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.