где h — величина подминаемого слоя металла, то получим
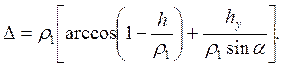 (38)
(38)
Известно, что процесс резания прекращается и металл
подминается индентором с радиусом ![]() при соотношении [19]
при соотношении [19]
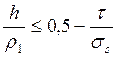 (39)
(39)
где ![]() — прочность на срез
связей контактирующих поверхностей в условиях температуры трения, Н/м2;
— прочность на срез
связей контактирующих поверхностей в условиях температуры трения, Н/м2;![]() — предел текучести обрабатываемого
материала, Н/м2.
— предел текучести обрабатываемого
материала, Н/м2.
С учетом выражения (39) формула (38) преобразуется к виду
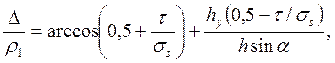 (40)
(40)
Если допустить далее, что величина характеризующая
степень пластического деформирования 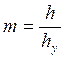 металла поверхностного
слоя, соизмерима с усадкой стружки, определяемой по формуле (17), то получим
металла поверхностного
слоя, соизмерима с усадкой стружки, определяемой по формуле (17), то получим
![]()
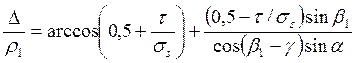 (41)
(41)
При обработке пластичных материалов можно принимать
![]() [28]. С учетом этого простого соотношения
из формулы (38) имеем
[28]. С учетом этого простого соотношения
из формулы (38) имеем
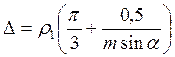 (42)
(42)
или при 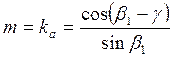
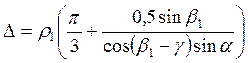 (43) Формула
(43) может быть представлена в виде
(43) Формула
(43) может быть представлена в виде
|
|
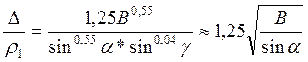 (44)
(44)
Формулы (41) и (44) показывают, что величина контакта на
задней поверхности неизношенного резца возрастает с увеличением радиуса
скругления режущей кромки резца р1 тангенса угла наклона плоскости
сдвига В и при уменьшении заднего угла ![]() .
Обращает на себя внимание интересный факт об увеличении контакта
.
Обращает на себя внимание интересный факт об увеличении контакта ![]() при уменьшении усадки стружки (при
возрастании В).
при уменьшении усадки стружки (при
возрастании В).
Работа с высокими скоростями резания ![]() и большими толщинами среза а1
при резании малотеплопроводных сталей и сплавов инструментальными материалами
низкой теплопроводности должна характеризоваться большими контактными площадками
на задней поверхности неизношенного инструмента, так как при этом
увеличивается В и, как следствие возрастают hy и
и большими толщинами среза а1
при резании малотеплопроводных сталей и сплавов инструментальными материалами
низкой теплопроводности должна характеризоваться большими контактными площадками
на задней поверхности неизношенного инструмента, так как при этом
увеличивается В и, как следствие возрастают hy и ![]() .
.
ОПРЕДЕЛЕНИЕ ВЕЛИЧИН ПОДМИНАЕМОГО СЛОЯ И УПРУГОГО ПОДНЯТИЯ МЕТАЛЛА
Если допустить, что
условная плоскость сдвига АВ проходит касательно к скругленной части режущей
кромки в точке А—точке разрыва металла при резании (см. рис. 7), то ![]() = <АОК и величина подминаемого слоя
металла h = ON—OK определяется
следующим образом [13, 24]:
= <АОК и величина подминаемого слоя
металла h = ON—OK определяется
следующим образом [13, 24]:
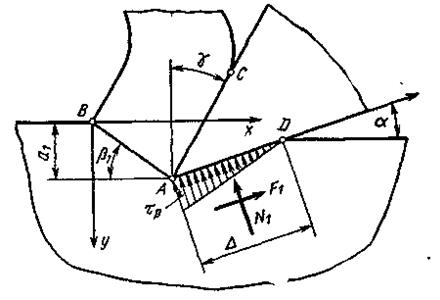
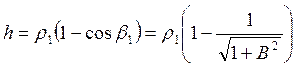 (45)
(45)
|
|
|
|
Рис. 10 Схема действия сил на задней поверхности инструмента
Допуская с определенным приближением справедливость равенства
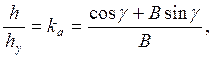 (46)
(46)
получим с учетом формулы (45) выражение для hy в виде
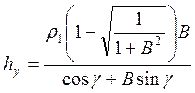 (47)
(47)
Формулы (45) и (47) показывают, что при резании материалов величины h и hy возрастают при уменьшении уcадки стружки (увеличении В), причем увеличение hy происходит значительнее, чем рост величины h.
СИЛЫ, ДЕЙСТВУЮЩИЕ НА ЗАДНЮЮ ПОВЕРХНОСТЬ ИНСТРУМЕНТА
В соответствии с исследованиями [34, 36] распределение касательных напряжений на задней контактной площадке инструмента может быть описано выражением
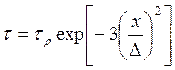 (48)
(48)
Интегрирование функции
(48) дает среднее касательное напряжение ![]() =0,505
=0,505![]() . Если на участке AD=
. Если на участке AD=![]() принять распределение касательных
напряжений по треугольнику с максимумом в точке А (рис. 10)
принять распределение касательных
напряжений по треугольнику с максимумом в точке А (рис. 10)
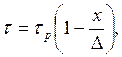 (49)
(49)
то среднее касательное напряжение ![]()
Так как средние касательные напряжения в рассмотренных случаях практически одинаковы, то принимаем упрощенный характер их распределения в соответствии с функцией (49).
Сила трения F1 определяется следующим образом:
![]()
С учетом формулы (44) окончательно имеем
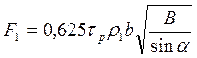 (50)
(50)
где b определяется для различных возможных случаев по формулам (6), (9), (12) и (15).
Для нормальной силы N1 на задней поверхности формула имеет вид 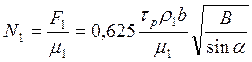 (51)
(51)
где ![]() —
коэффициент трения на задней контактной площадке.
—
коэффициент трения на задней контактной площадке.
Многочисленные исследования контактных процессов при резании показывают, что в физической природе протекания явлений трения и пластического деформирования на передней и задней поверхностях инструмента имеется много общего. Некоторое различие проявляется прежде всего в неодинаковости контактных температур на передней и задней поверхностях инструмента, а также в величине самих контактных площадок.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.