Машиностроение \ Основы резания металлов

Теоретическое определение параметров процесса резания ширина и толщина среза при несвободном резании. Теоретический метод определения обрабатываемости материалов резанием, страница 31

или                                                                                           

Если принять во внимайте, что относительная деформация тo

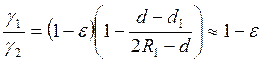
Следовательно, формула для относительной деформации имеет вид

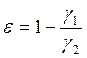                  (252)

Так как радиальные напряжения на поверхности всегда раины нулю, то согласно закону Гука тангенциальные напряжения на поверхности детали определяются выражением

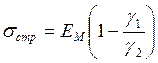                  (253)

Формула (253) показывает, что если вновь образовавшаяся фаза имеет больший объем и, следовательно, меньшую плотность γ2 по сравнению с γ1 то 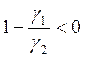и на поверхности детали возникнут остаточные напряжения сжатия.

Наоборот, если v2<v1 и γ2>γ1 то в поверхностном слое возникнут остаточные напряжения растяжения.

Плотности различных структурных составляющих сталей и сплавов приведены в табл. 15.

Таблица 15   

Плотность   структурных составляющих

Структура

Перлит

Троостит

Мартенсит

Аустенит

Феррит

Цементит

Плотность,кг/м3

7800

7808— 7830

7760

8160

7900

7700

Плотность мартенситовой структуры значительно меньше, чем плотность аустенита.     Удельные веса перлита и троостита занимают промежуточное положение между мартенситом и аустенитом. Таким образом, если при механической обработке, например закаленной стали с мартенситовой структурой в поверхностном слое, возникнет структура мартенсито-аустенита или мартенсито-троостита, то γ2>γ1  и формула (253) указывает на возможность возникновения остаточных растягивающих напряжений, так как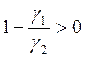.Наоборот, если после механической обработки в поверхностном слое образуется повышенный процент мартенсита или вообще структура с γ2<γ1  то в поверхностном слое возникнут остаточные напряжения сжатия.

 


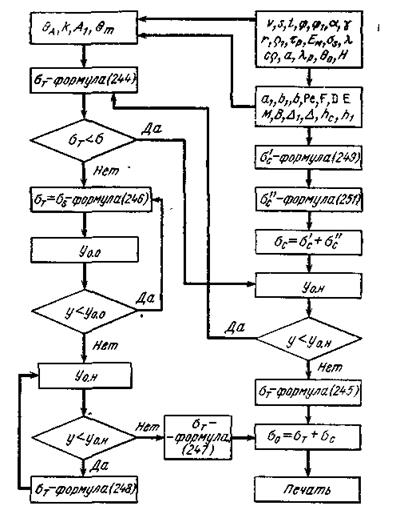Рис. 42. Блок-схема для расчета суммарных остаточных напряжений на ЭВМ   


Суммарные остаточные напряжения. Суммарные остаточные    напряжения определяются алгебраической суммой температурных, силовых и остаточных напряжений от структурных и фазовых превращений, т. е.

               (254)

где Следует отметить, что на данном этапе применение формулы (253) для количественного определения остаточных напряжений от структурных и фазовых превращений невозможно без экспериментального определения процентного содержания различных структур в поверхностном слое обработанной детали. Поэтому основные теоретические расчетные уравнения для остаточных напряжений были получены суммированием выше приведенных формул для температурных и силовых остаточных напряжений.

Теоретические зависимости для расчета суммарных остаточных напряжений получены в безразмерной критериальной форме, которая широко применяется в теории подобия. В общей сложности уравнения для суммарных остаточных напряжений учитывают около 20 различных технологических параметров, которые являются известными до опыта и объединены в 5—6 безразмерных комплексов, что придает им широкую общность и универсальность. Уравнения удобны для математического анализа и расчета на ЭЦВМ. Для расчета взаимосвязи величины остаточных напряжений и глубины их залегания с режимами резания на ЭЦВМ была разработана блок-схема, представленная на рис. 42 [44, 52].

 


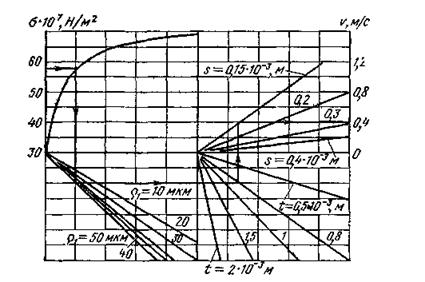Рис. 43. Номограмма для определения режимов резания по максимальному

значению остаточных     напряжений     при точении     жаропрочного     сплава.

ХН73МБТЮ резцами из сплава ВК8: γ=100 ; α=100 ; α1=100 ; φ=450 ; φ=150 ;λ=00


 


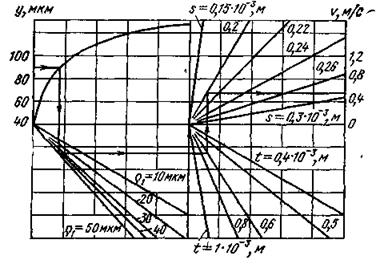
Рис. 44.  Номограмма для  определения  режимов резания  в зависимости  oт глубины    залегания  остаточных    напряжений    при  точении    жаропрочного сплава  ХН73МБТЮ  резцами  из  сплава   ВК8:

γ=100 ; α=100 ; α1=100 ; φ=450 ; φ=150 ;λ=00

Расчеты на ЭЦВМ позволяют для каждой пары резец— деталь получить номограммы, отражающие взаимосвязь величины и глубины залегания остаточных напряжений с режимами резания и геометрией инструмента. Две такие номограммы в качестве примеров приведены на рис. 43 и 44.                                                                                         

Скачать файл