при обработке стали 45 резцами из сплава Т15К6 в стружку при расчетных условиях уходит от 37,9 до 87,2% теплоты, в деталь от 47,4 до 11,9% и в резец от 14,7 до 0,9%;
при обработке титанового сплава ВТЗ-1 резцами из сплава ВК8 процент уходящей в резец теплоты значительно выше, чем при обработке стали 45, и может достигать при Pe<10 30—40%. При величинах Pe>60 этот процент также выше и составляет 5—7%. Количество теплоты Qд/Q при больших Ре также выше, чем при обработке стали 45.
Приведенные результаты теоретического исследования баланса тепла при резании в основе своей достаточно хорошо согласуются с результатами экспериментального и теоретического исследований других авторов [31, 36].
Подставляя в равенство (190) выражения (176), (182) и (189), получим уравнение энергий, включающее в себя температуру резания:
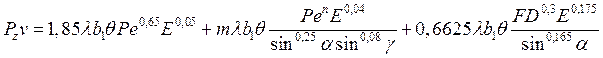
(19l)
Расчет баланса тепла по уравнению П91) при реальных значениях
критериев подобия: Ре=50; F=2; D=0.05; E=0.03; и ![]() и дал следующие результаты: Qc
и дал следующие результаты: Qc
=86 ; QД=11,6 и QР=2,4
ОБЩЕЕ УРАВНЕНИЕ ОБРАБАТЫВАЕМОСТИ
Ценность уравнения баланса энергий (191) состоит в том, что оно устанавливает связь скорости резания, входящей в критерий Ре, с различными технологическими параметрами. Путем специального анализа [40, 41] уравнение (191) приведено к виду
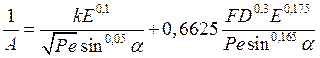
(192)
где
энергетический критерий, характеризующий собой тепловую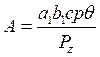 активность стружки по отношению ко всей выделяющейся в зоне резания
теплоте; k — коэффициент, учитывающий погрешность замены Pe0,43 на
активность стружки по отношению ко всей выделяющейся в зоне резания
теплоте; k — коэффициент, учитывающий погрешность замены Pe0,43 на ![]() , определяется из
табл. 7.
, определяется из
табл. 7.
Теоретическое критериальное уравнение (192) устанавливает зависимость Pe=f(A) (рис. 23), которая в двойной логарифмической сетке представляется в виде прямой линии или в виде ломаной линии с двумя прямолинейными отрезками.
С целью проверки точности критериального уравнения (192) выполнено сравнение критериальных зависимостей Pe=f(A) полученных расчетным методом по уравнению (192) и опытным путем. Результаты расчетов и опытов приведены на рис. 24— 26.
Анализ приведенных результатов сопоставления позволяет сделать вывод о вполне удовлетворительной точности критериального уравнения (192) и целесообразности его использования при разработке расчетного метода определения режимов резания.
Таблица 7.
Определение коэффициента k
|
Pe |
k |
Pe |
K |
|
1 2 5 10 20 30 |
2,85 3 3,2 3,3 3,5 3,6 |
40 50 76 100 150 200 |
3,7 3,75 3,85 3,9 4,05 4,1 |
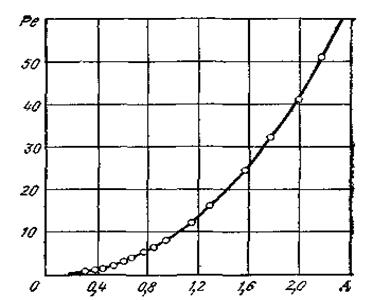
Рис. 23 Теоретическая зависимость Ре=f(A) при обработке стали 12Х18Н9Т резцами из сплава Т30К4 : γ=120; α=120; φ=450; φ1=150; s=0,1*10-3м; t=2*10-3м; r=0,5*10-3м; F=27м; D=0,022; E=0.09.
Скорость резания по уравнению (192) определяется двумя путями:
1. Расчетно-графическим методом с установлением степенной зависимости Ре=С1Аn и получением формулы для скорости резания в виде
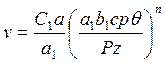 (193)
(193)
где C1 и п — числовые величины (см. рис. 24).
Например, на основе данных, приведенных на рис. 24—26, получены следующие уравнения обрабатываемости упрощенного вида:
при обработке стали 12Х18Н9Т резцами из сплава Т30К4
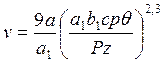 (194)
(194)
при обработке стали 4Х14Н14В2М резцами из стали P18
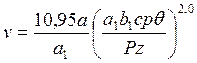 (195)
(195)
при обработке стали 45 резцами из сплава Т5К10
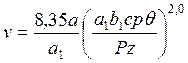 (196)
(196)
2. Расчетным методом с использованием решения уравнения (192) относительно критерия Ре в следующем виде:
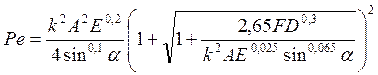 (197)
(197)
Для определения коэффициента k рекомендуется вначале ориентировочно по уравнению (197) определить критерий Ре при k=3,5, а затем по найденному значению Ре выбирается значение k.
Уравнение (197) содержит
скорость резания лишь в критерии 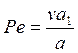 Решая уравнение (197)
относительно скорости резания v и подставляя вместо критериев подобия их соответствующие
выражения, получим общую формулу обрабатываемости сталей и сплавов в следующем
виде
Решая уравнение (197)
относительно скорости резания v и подставляя вместо критериев подобия их соответствующие
выражения, получим общую формулу обрабатываемости сталей и сплавов в следующем
виде
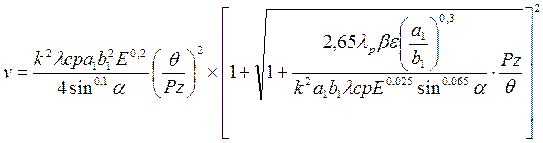
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.