Теоретическое определение параметров процесса резания ширина и толщина среза при несвободном резании. Теоретический метод определения обрабатываемости материалов резанием, страница 2

Совместное рассмотрение механических и тепловых явлений при резании материалов позволяет решить задачу по теоретическому определению угла наклона условной плоскости сдвига. Поперечная усадка стружки после этого определяется по формуле И. А. Тиме

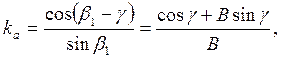                               (17)               

где— величина, характеризующая степень пластических деформаций металла снимаемого припуска и поверхностного слоя обрабатываемой детали;—передний угол резца.

Из анализа уравнения баланса механической и тепловой энергий при резании материалов для величины В может быть получено следующее теоретическое выражение (без учета влияния явлений трения на задней контактной площадке инструмента):

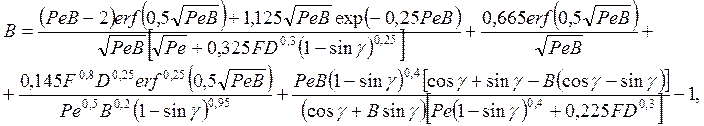    (18)

где Ре, F и D — безразмерные комплексы (критерии подобия), определяющиеся выражениями:

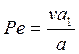 —  критерий Пекле,    характеризующий степень влияния режимных условий процесса по сравнению с влиянием теплофизических свойств обрабатываемого материала ;

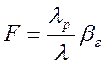 — критерий, отражающий влияние геометрии инструмента и отношения теплопроводностей инструментального и обрабатываемого материалов;

D = a₁ / b ₁  — критерий, характеризующий геометрию сечения среза.

Входящие в критерии Ре, F и D и в уравнение (18) параметры имеют следующие смысл и размерность:

 — скорость резания, м/с;

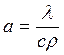 и —коэффициенты теплопроводности инструментального и обрабатываемого материалов, Дж/(м-с-град);—коэффициент температуропроводности обрабатываемого материала, м²/с; ср — удельная объемная теплоемкость обрабатываемого материала, Дж/(м³-град);

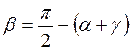 —угол заострения резца, рад.; и—задний и передний углы резца, рад.;—угол при вершине резца в плане, рад.;

 и —главный и вспомогательный углы резца в плане, рад.;

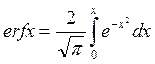  —   интеграл вероятности, функция, хорошо табулированная в литературе [39] и др. Изменение этой функции в зависимости от критериев подобия Ре и В, характеризующих процессы резания, представлено на рис. 4.

Приближенные степенные формулы для определения значения функции в зависимости от Ре В получены в виде

 

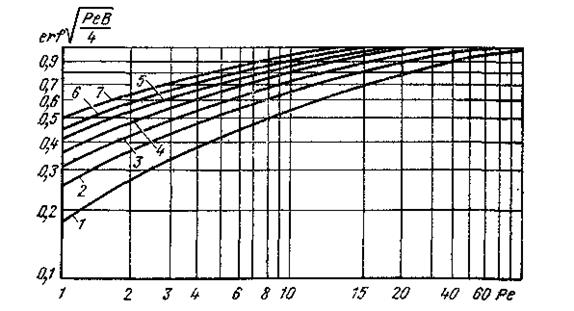Рис. 4. Зависимость функции 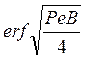от критериев Ре и В:

1 — В=0,1;   2 — В=0,2;    3-В = 0,3;    4-В=0,4;    5 — В-0,5;    6 — В-0,6;    7-В=0,7

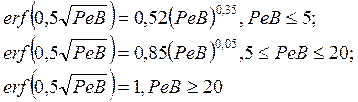
Все параметры, входящие в уравнение (18), являются известными до опыта. Искомый параметр В входит во многие члены левой и правой частей уравнения (18), и теоретическое определение этого параметра (усадки стружки) обычным методом затруднительно. Однако эта задача сравнительно легко решается с помощью электронно-вычислительных машин. Для случая соответствующего рациональным режимам резания, из уравнения (18) получена более простая теоретическая формула степенного вида [46]      

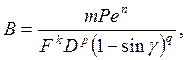                                 (19) в которой коэффициент m и показатели степени n, k, p и q .В зависимости от условий выполнения процессов резания должны определяться по табл. 1.   Располагая известными до опыта величинами , a_1, b_1, a, , , ,  и  ,расчетом можно  определять безразмерные комплексы Ре, F, D, и далее при выбранных значениях m, n, k, p и q из табл. 1 находится величина тангенса угла наклона плоскости сдвига В.

Числовой   пример  1.   Требуется определить    расчетным    путем В при  следующих  условиях  обработки  точением  стали  40Х  резцами  с  пластинками из сплава Т15К6  v=2,5    м/с;  a₁ = 0,l*10^-3  м;  b₁=3*10-³ м;   = 10°; =10°;  =45°;  =15°;  а=6,75*10^-6 м²/с;    =27,2    Дж/(м*с*град);    =33,9 Дж/(м*с*град);               При  этих  данных   имеем     Ре=37;     F== 1,535;   D = 0,033; () = 0,826;                                          

                

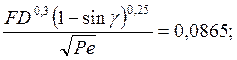
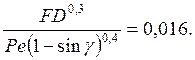
Из табл.  1  находим m=0,11, n=0,28; k=0,12; р= 0,03;  q=1,35    и    получаем значение

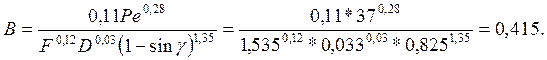
Поперечная усадка стружки при этом равна

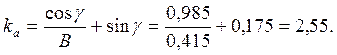
Числовой   пример   2     Точение    титанового    сплава    АТЗ-1    резцами с пластинками   из   ВК8  Значения   параметров   , a₁, , ,  и — те же, что и в примере 1, но =58,5   Дж/(м*с*град);    = 13.45 Дж/(м *с*град);   а=4,9*10-⁶ м²/с

Таблица   1  

Постоянные величины для определения тангенса  угла  наклона условной плоскости сдвига