4) создать экспериментальную установку, оснащенную необходимыми приборами, позволяющими одновременно измерять все параметры, которые являются неизвестными до опыта и входят в неопределяющие критерии;
5) провести опыты при условиях выбранных значений величин, входящих в определяющие критерии, с фиксированием значений параметров неопределяющих критериев;
6) произвести расчет числовых значений определяющих и неопределяющих критериев подобия и их обработку методами математической статистики (например, методом наименьших квадратов) с целью получения конкретной количественной связи между неопределяющими и определяющими критериями (критериальные уравнения).
Например, если экспериментальные точки в логарифмических координатах хорошо ложатся на одну прямую линию, то критериальные уравнения при резании принимают следующий степенной вид:
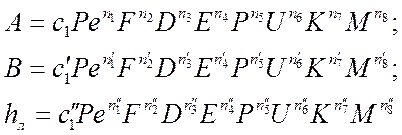(268) (269) (270)
и т. д.
Получаемые на основе всего лишь нескольких опытов таким образом критериальные уравнения обладают большой общностью, так как они объединяют собой большое количество групп подобных между собой явлений: каждой одной экспериментальной точке соответствует своя группа подобных явлений, определяемых различными комбинациями численных значений параметров, входящих в критерии подобия. Рассмотрим получением критериальной зависимости А=f(Ре, F, D... M).
При экспериментальном определении обрабатываемости на конкретной операции механической обработки обычно деталь и инструмент являются неизменными, что позволяет исключить» из рассмотрения критерия Р, U и К. При выбранном инстру-ментальном материале также не должен учитываться критерий F. Проведенное большое количество опытов показало так же, что изменение критериев подобия D, E и М в возможных пределах вызывает незначительное поле рассеяния эксперимен-тальных точек основной зависимости A=f(Pe) или Pe=f(A). Последнее объясняется малыми значениями показателей при критериях Д и Е и сравнительно умеренным влиянием на характер зависимости Ре=f(А) второго слагаемого правой части уравнения (192). Таким образом, можно приближенно считать, что для выбранной пары резец — деталь характер зависимости A=f(Pe, D, Е) определятся в основном зависимостью А=f(Ре) или Ре=f(А), Поэтому при экспериментальном изучении процессов обработки, когда рассматриваются конкретные деталь и резец, в большинстве случаев достаточно вообще oограничиться двумя критериями А и Ре и получением зависимости вида:
(271)
или
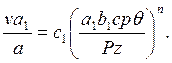
Для оптимальной скорости резания имеем
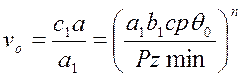(272)
На основании вышеизложенного основные положения новой методики экспериментирования могут быть сформулированы следующим образом:
1) эксперименты при изучении термомеханических явлений и вопросов обрабатываемости материалов резанием необходимо ставить таким образом, чтобы после проведения каждого опыта были известны числовые значения всех величин, входящих в критерии А и Ре;
2) подсчитывать числовые значения критериев А и Ре;
3) результаты расчетов величин А и Ре нанести в виде экспериментальных точек на двойную логарифмическую сетку, причем значение критерия А откладывается по оси абсцисс, а критерия Ре — по оси ординат;
4) после проведения намеченной серии опытов и обработки результатов указанным выше методом установить критериальную зависимость вида (271).
Заметим, что величины ср и а являются известными до опыта, так как они выбираются для соответствующего обрабатываемого материала из имеющихся справочников. Параметры режима резания v, a1 и b1 также являются известными до опыта, так как величины v, s и t обычно выбираются заранее. При заданной геометрии инструмента (φ, φ1 , r) и выбранных t и s величины a1 и b1 определяются расчетом по формулам, приведенным в гл. I. Следовательно, во время самих опытов следует определять одновременно две оставшиеся величины: температуру резания θ и тангенциальную составляющую силы резания Pz. Поэтому все нижеописанные экспериментальные исследования проведены автором в виде опытов с одновременным измерением величин θ и Pz. В ряде серий опытов производилось также измерение усадки стружки, радиального износа инструментов, свойств качества поверхностного слоя и др.
ЭКСПЕРИМЕНТАЛЬНАЯ АППАРАТУРА
Для измерения силы Pz применен однокомпонентный динамометр, позволяющий определять силу независимо от длины вылета резца (рис. 45). Длительная эксплуатация описанного выше динамометра показала его большую надежность в работе, простоту обслуживания и хорошую стабильность показаний. Динамометр может быть широко использован не только в лабораторных, но и производственных условиях.
При проведении исследований процессов точения и фрезерования на автоматизированных станках и станках с ЧПУ широко использовался для измерения сил Pz, Рy и Рх трехкомпонентный динамометр УДМ600 конструкции и производства ВНИИ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.