Учитывая фактор зависимости и независимости событий, можно уточнить формулу сложения для двух совместных событий.
р(А+В)=р(А)+р(В)-р(АВ),
тогда для совместных
-независимых событий р(А+В)=р(А)+р(В) – р(А)*р(В)
-зависимых событий р(А+В)=р(А)+р(В) – р(А)*р(В/А)
Домашнее задание: 1.Студент 6 раз купил напиток, 5 раз купил игрушку. Девушка заметила, что 3 раза он приходил одновременно с игрушкой или напитком. Является ли покупка игрушки и напитка зависимым или независимой. Всего ходил 10 раз.
2.Из колоды 36 карт вытаскивают туз. Является ли зависимым событие вытащить пиковую карту и пикового туза.
nк=36, nпики=9, nт=4
р(АВ)=р(А)*р(В) – независимые
р(А)=1/9 р(В)=1/4
1/36=(1/9)*(1/4) события независимые.
Задача: Пусть дано 20 чисел и событие А состоит в том, что из 20 чисел выбирается четное число. Пусть событие В состоит в том, что из 20 чисел четное число делится на 3.
1.Какова вероятность того, что число будет делиться на 2 и сколько таких чисел?
2.Какова вероятность того, что число будет делиться на 3 и сколько таких чисел?
3.Какова вероятность того, что число будет делиться и на 2, и на 3 одновременно и сколько таких чисел?
4.Являются ли события А и событие В зависимыми или независимыми?
Решение:
1.чисел 10; р(А)=5/10
2.чисел 6; р(А)=6/20=3/10
3.чисел 3; р(А)=3/20
4.р(АВ)=р(А)*р(В) независимые события
3/20=5/10*3/10, значит события А и В независимые.
2.7.Частные случаи зависимости и независимости событий
Зависимость и незавсимость событий с достоверным и невозможным событием определяется следующими правилами:
1.Любое событие А с достоверным невозможным событием является независимым.
р(А/U)=р(А)
р(А/V)=Р(А)
р(U/А)=р(U)
р(V/А)=р(V)
Это обусловлено тем, что достоверное невозможное событие не зависит от того, произошло ли событие А или нет.
Безусловная вероятность= условной вероятности:
р(А)=р(А/В)
2. Если события А и В
независимые, то![]() и В тоже независимые, А и
и В тоже независимые, А и ![]() тоже независимые,
тоже независимые, ![]() и
и
![]() тоже независимые.
тоже независимые.
3.События могут быть попарно независимы: А и В независимы, В и С независимы, А и С независимы.
4.События могут быть независимы в совокупности:
А1, А2,…,Аn – не зависят друг от друга.
Независимость в совокупности более сильное требование, чем попарная независимость.
2.8.Связь несовместных и совместных событий с независимыми и зависимыми
Не следует путать несовместность и совместность событий с их независимостью и зависимостью.
1.Несовместность и совместность событий означает могут ли события произойти одновременно или нет. Это обстоятельство определяется физическим и здравым смыслом.
2.Независимость и зависимость событий означает, что появление одного из событий влияет на вероятность появления второго. Это свойство определяется математическим, но не здравым смыслом.
Теорема: Если события А и В несовместны (и имеют некоторую вероятность), то они обязательно зависимы.
Доказательство от противного:
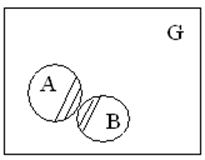
Если события несовместны
р(АВ)=V=0
Если предположить, что события независимы, то
р(АВ)=р(А)*р(В)=0
Это возможно, если р(А)=о, либо р(В)=0, либо обе вероятности = 0.
Это противоречит условию, т.к. р(А)>0, р(В)>0, значит события зависимы.
Для совместных событий условие соблюдается ограниченно.
Совместные события могут быть, как зависимы, так и независимы; несовместные события могут быть только зависимыми.
Следовательно, существует определенная связь между совместностью и несовместностью и их независимостью и зависимостью.
2.9.Обсуждение результатов
Из алгебры событий следует, что:
1.Наступление одного из событий определяется теоремами сложения.
р(А+В)=р(А)+р(В)
р(А+В)=р(А)+р(В)-р(АВ)
При этом вторая формула
р(АВ)=р(А)*р(В) для совместных независимых событий.
р(АВ)=р(А)*р(В/А) для совместных зависимых событий.
2.Вероятность одновременного наступления событий определяется теоремой умножения.
р(АВ)=р(А)*р(В) для независимых событий.
р(АВ)=р(А)*р(В/А) для зависимых событий.
р(АВ)=р(В)*р(А/В) для зависимых событий.
3.Вероятность события р(А) всегда < 1.
р(А)<р(U)<1,
т.к. А![]() U.
U.
Событие А является частным случаем достоверного события.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.