Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 21

1.Плотность распределения распределена на всем интервале от -до + и является положительной величиной, т.к. первая производная от функции распределения является положительной (функция распределения монотонно возрастает, отсюда следует, что первая производная положительна).

2.Плотность распределения симметрична относительно оси ординат, т.к. отклонение определяется квадратом (х-m_x)².

3.Плотность распределения имеет некоторый max, соответствующий МО.

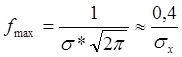
4.При Х (по абсолютной величине)ветви кривой плотности распределения асимптотично приближаются к оси абсцисс.

5.Кривая плотности имеет 2 точки перегиба:

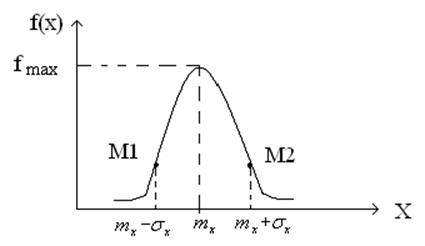
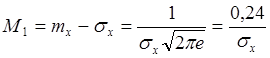
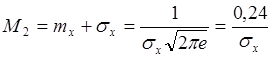
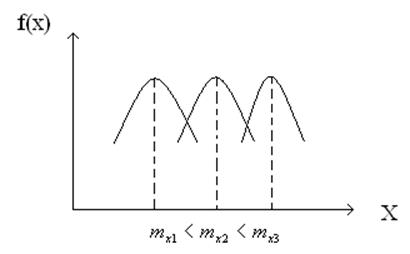
6.При изменении МО и const СКО кривая смещается:

 

7.Если МО=const, а СКО изменяется:

 

Чем больше (СКО), тем больше упрощается функция распределения и ее максимум становится меньше.

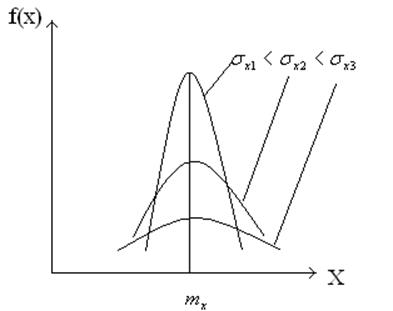
Это обусловлено тем, что неопределенность возрастает. Уплощение функции происходит из-за того, что площадь, ограниченная  плотностью распределения, всегда =1.

4.9.Определение вероятности попадания СВ в заданный интервал

Если требуется найти вероятность попадания СВ Х в некоторый интервал [a,b], то необходимо найти площадь ограниченную плотностью распределения на этом интервале.

Для нормального распределения:

р(a<x<b)=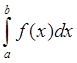

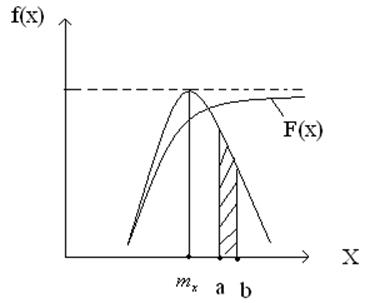
Эта вероятность равна интегралу от плотности распределения.

Этот интеграл относится к категории неберущихся, т.е. не выражается в элементарных функциях, он называется интегралом Лапласа или интеграл вероятности.

В реальных расчетах используются его табулированные значения, которые обозначаются символом Ф, тогда:

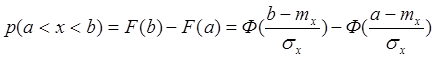
Ф – табличное значение интеграла вероятности.

4.10.Правило трех сигм (3)

ЗНР обладает замечательным свойством таким, что вероятность попадания в некоторый интервал, исчисляемый количеством СКО, заранее известна.

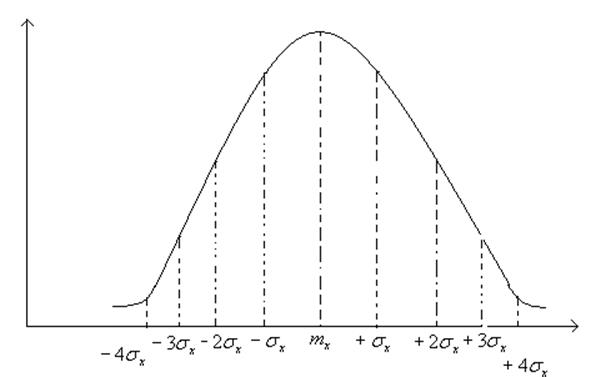
р()=0,682

р()=0,954

р()=0,973

Приведенные числа показывают, что вероятность попадания СВ в интервал  =0,997, т.е. только 3 шанса на 1000, что событие не состоится.

0,997 – надежная вероятность;

0,95 – инженерная вероятность;

0,68 – вероятность с положительной динамикой (небольшой перевес);

0,5 – соответствует МО – азартная игра с природой.

Если вы считаете, что вероятность  недостаточно, то можно вероятность .

То есть 6 шансов на 100000, что событие не состоится.

4.11.Применение правила трех сигм

Правило  широко применяется в инженерных и профессиональных дисциплинах при условии, что реализуется гипотеза о нормальном ЗР. Это обусловлено тем, что суммирование любых ЗР (о чем речь пойдет ниже) приводит к закону нормального распределения.

В технике правило  применяется в двух аспектах:

1.Дано:

Определить:

Тогда принято считать, что , а .

р=0,9973

Пример: мощность двигателя в среднем при колебании нагрузки составляет 30 кВт (). При этом СКО колебаний нагрузки .

Определить max и min мощности двигателя.

Тогда р_max=36 кВт, а р_min=24 кВт с вероятностью р=0,9973.

2.Дано:

Определить:

Пример: напряжение в квартире измеряется в пределах 232В = U_max, 208В =  U_min.

Получается, что .

СКО определяется как интервал отклонений деленный на 6.

Таким образом, правило  позволяет определить как пределы, так и пределы отклонений СВ, так и сами числовые характеристики.

4.12.Нормальный ЗР и интеллект

С момента возникновения человека разумного возник вопрос измерения его интеллекта, при этом всегда следует помнить, что интеллект и образование не одно и то же, но они способствуют друг другу. Между ними имеется положительная корреляция. Измерение интеллекта в настоящее время осуществляется с помощью некоторых тестов Стекфорда-Бинэ. При этом определяется коэффициент интеллекта (Intelligent Quality IQ). Было показано, что интеллект также распределяется по нормальному ЗР.

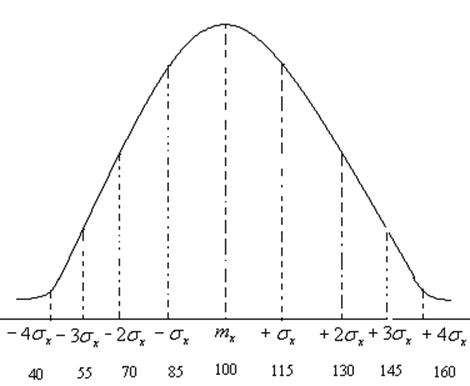
Баллы IQ	Вербальная оценка	Примечание
85-115	нормальные	таких 68%
умные		правая ветвь
115-130	способные
130-145	одаренные	2-1 человек на 1000
145-160	сверходаренные	3 человека на 100000
160 и больше	гении	1 человек на 1000000
слабоумные		левая ветвь
70-85	малоспособные	5 на 1000
55-70	бездарные	1-2 человека на 1000
40-55	дебильные	3 человека на 100000
25-40	имбициллы (кретин)	1 человек на 1000000
меньше 25	идиоты