В целом следует отметить, что полученные соотношения практически не зависят от континентов и рас. Следует иметь ввиду, что тесты IQ позволяют частично приспособиться к ним, если многократно решать эти задачи.
4.13.Функция одной СВ и ее распределение
На практике часто возникает задача определения некоторой функции У от случайного аргумента Х.
![]() ,
,
где Х – некоторая СВ.
Задача решается по разному для ДСВ и НСВ.
1.ДСВ обычно задается в виде ряда распределения, т.е. значения Х и соответствующих им вероятностей.
Без утраты общности рассмотрим пример:
![]()
Дано:
|
х |
х1 |
х2 |
|
р |
0,8 |
0,2 |
Пусть
х1=2, а х2=3, тогда ![]() вероятности
р=0,8 и р=0,2.
вероятности
р=0,8 и р=0,2.
Примечание: вероятности сохраняют свое значение.
2.Для НСВ выводится следующая формула (мы этого делать не будем) для плотности распределения Y.
![]() , (*)
, (*)
где ![]() - функция обратная
- функция обратная ![]() .
.
Алгоритм:
1.Записывается ![]()
2.Находится функция ![]() обратная
Х
обратная
Х
![]()
3.Определяем плотность распределения от обратной
функции ![]() .
.
4.Определяем производную от обратной функции по
абсолютной величине. ![]() .
.
5.Подставляем в исходную функцию (*).
Формула работает, если функция дифференцируема. Иногда для функции первого аргумента можно найти по числовым характеристикам, что гораздо проще.
Например, часто Y имеет линейную зависимость от Х.
![]() ,
,
где А – оператор преобразования = const.
Тогда ![]()
![]()
Полученные значения числовых характеристик подставляем в ЗР.
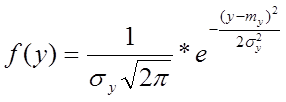
4.14.Композиция ЗР
Если функция является зависимой для 2х СВ Х,Y z=X+Y, то X,Y могут иметь ЗР.
Пример: ошибка измерения прибора подчинена НЗР, а ошибка округления при считывании прибора подчинена равномерному ЗР. Тогда для плотности распределения:
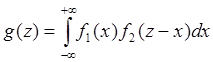
Сложение ЗР называется их композицией. Устойчивые композиции такие, которые при сложении законов не изменяются (не изменяется вид распределения).
Пример: нормальный ЗР.
Если же при сложении вид распределения меняется, то композиция называется неустойчивой.
Пример: сложение равномерных законов изменяет распределение, а именно слоение 2х равномерных законов дает треугольный ЗР (закон Симпсона), а сложение 3х равномерных ЗР дает НЗР.
4.15.Обсуждение результатов
1.Выше были рассмотрены ЗР одномерных непрерывных СВ. ПРИ этом следует иметь в виду, что основой этих теоретических распределений служит некоторый эмпирический закон случайностей (эмпирический, значит полученный из опытов).
Так, например, равномерный ЗР вытекает из округления показаний и фазы включения.
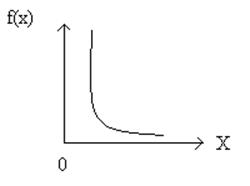
Показательный (экспоненциальный) вытекает из случайного времени наработки на отказ.
Нормальный ЗР обобщает ошибки измерений.
Закон Релея характеризует плотность распределения угла наклона (крена) кораблей при качке.
Не следует верить тем, кто считает, что ТВ дает неоднозначные и размытые результаты, на самом деле ТВ из хаоса случайных явлений позволяет вывести строгие суждения. При этом во многих случаях и в том числе в случаях первостепенной важности ТВ позволяет предсказать такие результаты и с такой точностью, с какой не может сравниться ни какое обычное предвидение, основанное на знаниях. При этом следует учитывать, что с увеличением числа испытаний частота встречаемых явлений устанавливается и стремится к значению вероятности тем самым, приобретая хорошую устойчивость результатов.
2.Следут иметь в виду, что СВ при суммировании дают также либо устойчивое, либо неустойчивое распределение.
Пример: равномерный закон
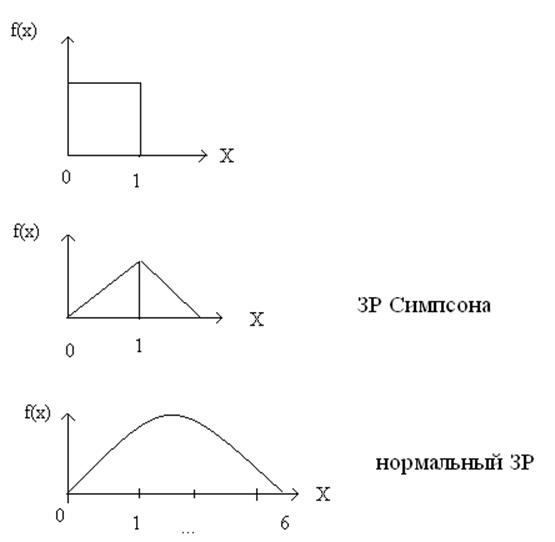
Сложение показательного ЗР приводит к закону Эрланга.
Суммирование нормального ЗР дает нормальный ЗР.
В общем случае суммирование законов любой природы, если каждая СВ не значительна приводит к нормальному ЗР в соответствии с предельной теоремой Ляпунова.
3.При нормальном ЗР полезно помнить, что отклонение СВ в одну сторону округленную в % имеет следующие значения:
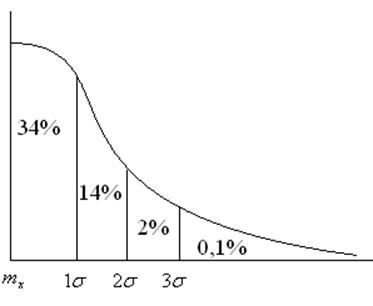
Таким образом, приращение вероятностей отклонений быстро убывает.
5.1.Понятие системы 2х СВ (С 2х СВ)
Ранее нами рассматривались случайные события результатом которых были некоторые СВ. Т.к. это значение СВ определялось одним числом, то они называются одномерными. Однако в инженерной практике существуют условия, когда результатом того или иного опыта (эксперимента) являются 2 и более СВ.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.