Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 19

Физическая природа ЗР ограничивает область из применения теми или иными инженерными задачами. Так, например, равномерный ЗР соответствует округлению показаний прибора при считывании значений параметра по его шкале.

Экспоненциальный ЗР характеризует время наработки на отказ в технических системах и широко применяется в теории надежности.

Нормальный ЗР характеризует отклонение размеров детали, ошибку любых измерений, оценку влияния большого числа факторов, а также отклонение электрической нагрузки.

Известно также, что ЗР вероятности наклона при качке корабля подчиняется закону Релея.

4.2.Закон равномерного распределения

НСВ имеет равномерный ЗР на отрезке [a,b], если плотность распределения СВ Х на этом интервале постоянна, а вне его =0.

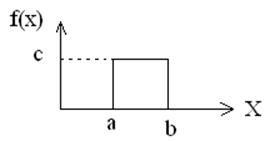
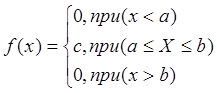
Возникает вопрос, какова величина с=const? Известно что

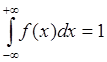 (второе свойство плотности распределения).

Это значит, что площадь, ограниченная плотностью распределения, есть вероятность. В данном случае для отрезка существования СВ.

,

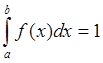где f(x)=c, тогда с=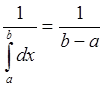

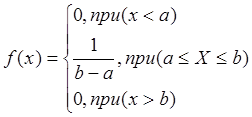
Определим числовые характеристики.

1.M[X]= m_x=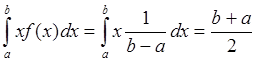

Что подтверждает интуитивное представление (середина отрезка).

2.D[X]=D_x=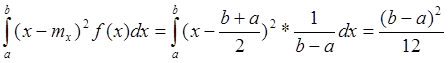

Удобнее оперировать СКО:

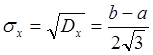
Найдем другие числовые характеристики

1.Mediana.

М_е=m_x

2.Moda.

M₀=0

3.Коэффициент асимметрии.

A_s=0, т.к.

4.Эксцесс.

Е_х=-1,2

 

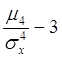
Это означает, что закон имеет более плоскую фигуру, чм стандартный нормальный ЗР.

Иногда по плотности распределения приходится определять функцию распределения.

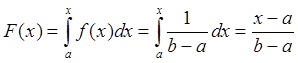
Графически это означает, что функция распределения возрастает линейно от a до b.

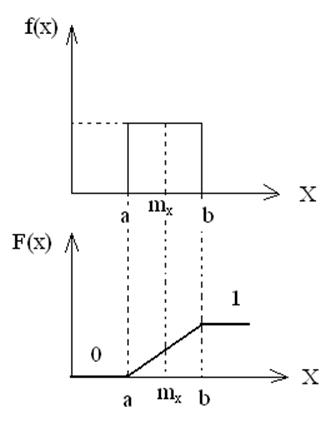
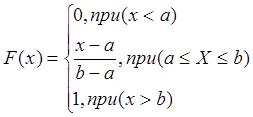
Иногда бывает необходимость найти вероятность попадания СВ распределенной равномерно в некотором интервале :

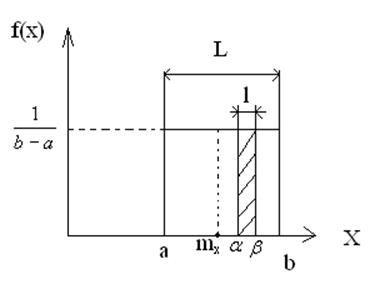
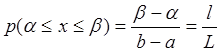
То есть отношение отрезков (размеров) есть геометрическая вероятность.

Таким образом, равномерный закон распределения является достаточно простым, симметричным, а его характеристики и вероятности попадания могут быть определены, как соотношение размеров.

4.3.Закон показательного распределения СВ

(Экспоненциальный закон распределения)

Закон показательного (экспоненциального) распределения НСВ имеет плотность распределения, определяемую следующим выражением:

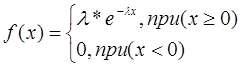
Для простоты можно писать

,

где- целое положительное число, остающееся неизменным.

=const, >0

Очевидно, что закон определяется затухающей экспонентой.

Функция распределения будет равна:

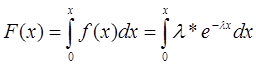
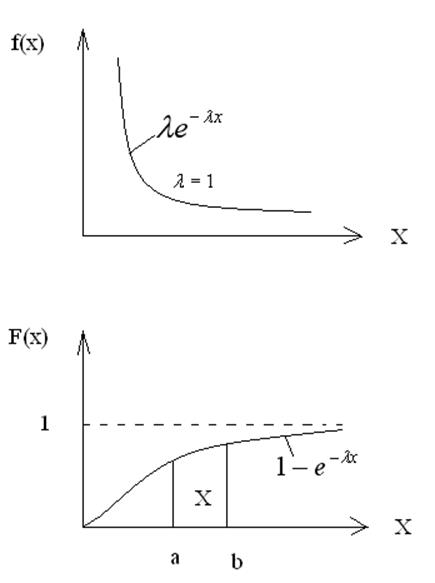
Если требуется найти вероятность попадания Х в некоторый заданный интервал [a,b], то эта вероятность равна

Примечание: первой частью является функция от a, второй – функция от b.

Определим числовые характеристики показательного закона распределения:

1.МО

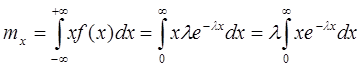
Предполагая, что при   убывает быстрее, чем любая степень х, тогда .

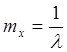Иначе говоря, МО экспоненциального ЗР обратно пропорционально постоянной .

2.Дисперсия

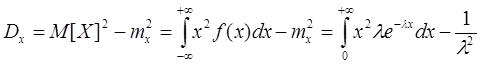
Это дает 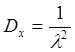, переходя к СКО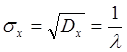   

Мы получили феноменальный результат, что

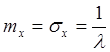
Отсюда следует, что показательный ЗР зависит только от одного параметра ; коэффициент вариации 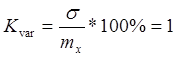 (100%) тоже единственный

С физической точки зрения, это означает, что вариация СВ равна ее МО. Это можно считать некоторой нормой случайности.

Если , то можно сказать, что СВ имеет меньшую случайность, а если , то СВ имеет большую случайность, чем норма.

3.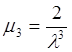, тогда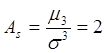

Этого следовало ожидать, т.к. показательный ЗР имеет только правый «хвост» распределения, что приводит к положительной асимметрии.

Закон показательного распределения, таким образом, является асимметричным и не имеет Moda. На практике часто возникает проблема в связи с тем, что  неизвестна, кроме того, требуется доказательство, что это есть показательный закон. В этом случае рекомендуется 2 действия:

1.По некоторой выборочной статистике определяется среднее (МО), которое находится в соотношении с  следующим образом:

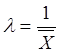
Отсюда, хотя и приближенно находится константа .

2.Если по выборочной статистике будут выбраны среднее (МО) и СКО () и они будут примерно равны , то закон распределения СВ является показательным.

4.4.Закон показательного распределения в теории надежности

Показательный ЗР играет исключительно большую роль в технике при оценке надежности работы, как отдельных элементов системы, так и технической системы (ТС) в целом.