где U – напряжение.
Пусть на числовой оси СВ Х заданы некоторые ее конкретные значения х1, х2,… хi,…, хn, соответствующие им вероятности.
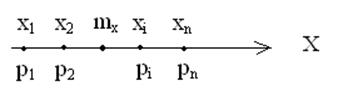
Тогда, МО ДСВ есть сумма произведений всех возможных значений СВ на вероятности этих значений.
М[X]= mx=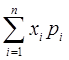
С физической точки зрения, МО представляет собой некоторое средне взвешенное среднее, которое соответствует центру тяжести в механике, где в нашем случае хi – некоторое плечо, рi – некоторый вес. Иначе говоря, каждая величина входит в среднее значение со своим весом.
Отсюда следует, что
МО есть некоторая точка, обеспечивающая устойчивость (равновесие) всей
технической системы. Эта точка характеризует также некоторое средне взвешенное
значение относительно которого СВ группируются (рассеиваются) случайным
образом. В частном случае может быть счетное множество СВ может распределиться
до ![]() .
.
М[X]= mx=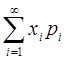
Следует иметь в виду, что ряд, находящийся справа не всегда сходится и МО может быть =0. Однако в технических дисциплинах это не случается, т.к. имеет конечное значение.
Следует иметь в виду, что значения вероятностей зависят от величины выборки:
М[X]=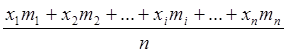 ,
,
где m1, m2,… mi,…, mn – число благоприятных опытов каждой из СВ,
тогда 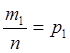 ,
, 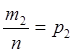
Тогда
М[X]=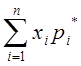 ,
,
где ![]() - статистическое число вероятности
- статистическое число вероятности
![]()
В связи с этими рассуждениями можно заметить, что МО не равно среднему арифметическому. Однако с увеличением числа опытов среднее арифметическое стремится к МО.
В связи с этим во многих случаях, если вероятности неизвестны или они равновозможны в качестве оценки МО принимается среднее арифметическое, а в математической статистике оценивается полученная погрешность.
Для НСВ МО является интегралом
М[X]= mx=![]()
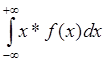
В частном случае, если СВ Х ограничена отрезком [a;b], то интеграл берется в этих пределах.
МО является чрезвычайно применимым термином в ТВ, т.к. позволяет дать некоторые устойчивые оценки любых параметров.
Наряду с МО существуют еще 2 числовые оценки положения СВ:
1.Moda – значение СВ, которой соответствует наибольшая вероятность.
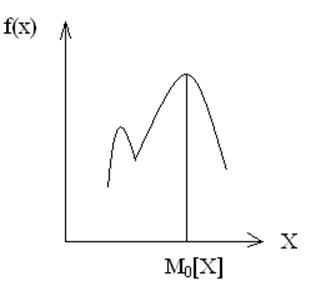
2.Mediana – значение СВ по отношению к которой вероятность попадания СВ как большую, так и в меньшую сторону равна 1/2.
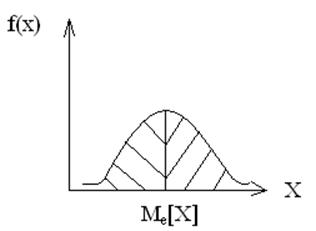
р(Х<Ме)=р(Х> Ме)=1/2
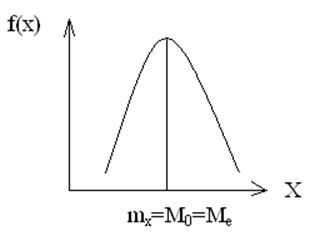
3.Для унимодальных (симметричных одновершинных) функций распределения плотности симметричны.
Все 3 характеристики совпадают:
3.16.Свойства МО
1.МО константы = самой константе.
М[C]=C, С=const
Док-во: М[С]=C*pc=C*1=C
2.МО нуля равна нулю. Это вытекает из предыдущего свойства.
М[0]=0
3.Любую переменную можно выносить за оператор МО.
М[CX]=C*M[X],
где C=const
4.МО произведения двух независимых СВ = произведению их МО.
М[X*Y]=M[X]*M[Y]
Примечание: легко распространяется на любое число НСВ.
5.МО суммы (разности) двух СВ равно сумме(разности) их МО
М[X![]() Y]=M[X]
Y]=M[X] ![]() M[Y]
M[Y]
6.Если ко всем СВ
прибавить (отнять) некоторую константу, то МО искомой величины равно МО от Х ![]() постоянная С.
постоянная С.
М[X![]() С]=M[X]
С]=M[X] ![]() С
С
7.МО отклонения СВ от своего МО =0.
М[X- mx]=0
Док-во: т.к. mx=const, обозначим ее mx=С
М[X-С]=M[X] – С=С – С=0
В реальных вычислениях величина МО часто центрируется.
![]() - центрированная СВ.
- центрированная СВ.
Тогда из 7-го
свойства следует, что МО ![]() =0
=0
[![]() ]=(Х- mx)
]=(Х- mx)
М[![]() ]=М[Х- mx]=0
]=М[Х- mx]=0
3.17.Частные случаи
Часто приходится вычислять МО наступления события в n независимых испытаниях, если известна вероятность наступления события в первом испытании.
![]() М[Х]= mx=n*p
М[Х]= mx=n*p
Пример: студент в течение года сдает 10 экзаменов с вероятностью р(А)=0,6. Отсюда следует, что МО = n*p=10*0,6=6. Иначе говоря, для биномиального закона распределения СВ МО mx=n*p.
3.18.Дисперсия СВ
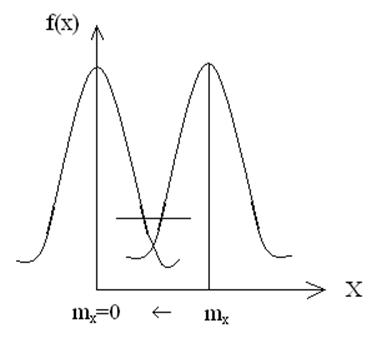
В действительности часто возникают случаи, когда МО двух СВ примерно одинаковы, однако сама СВ относительно них рассеивается по разному. Таким образом, необходимо ввести новую числовую характеристику, характеризующую это рассеивание, она называется дисперсия, в точном переводе «рассеивание», является некоторым МО величины отклонения.
Дисперсия – МО квадрата отклонения СВ от ее МО.
Dх= М[Х- mx]2,
где Dх – дисперсия.
Dх= М[![]() ]2 – для центрированной СВ.
]2 – для центрированной СВ.
для ДСВ: Dх=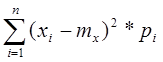
для НСВ: Dх=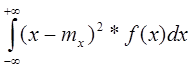
Дисперсия в какой-то степени характеризует неопределенность СВ, исходя из того, что чем больше разброс, тем больше неопределенность.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.