Иначе говоря, событие А и В
наступают одновременно.
4.Разностью двух событий
называется событие, в площадь которого входит событие В, но не принадлежит
событие В (верно и обратное).
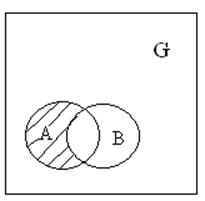
А – В или А\В
С физической точки зрения, разность означает: из наступления события А вычитается событие В.
5.Несовместными называются события, которые не могут произойти одновременно – не встречаясь в единичном опыте.
Пример: попадание и промах.
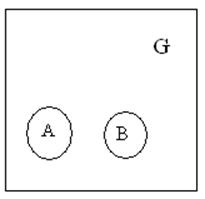
А*В=0 
6.Достоверным событием называется событие, которое наступает обязательно.
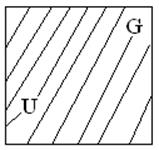
р(U)=1
Любая произвольно выбранная точка не может оказаться вне пределах области G.
7.Невозможным событием называется такое, которое никогда не происходит.
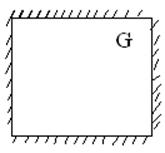
Р(V)=0 V=0
Любая произвольно выбранная точка не может попасть в заданную область G.
8.Полная группа событий – это совокупность всех событий, совпадающих с пространством всех элементарных событий G.
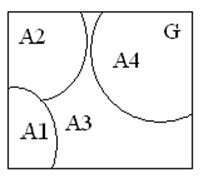
А1+А2+А3+А4=G
Для полной группы событий характерно то обстоятельство, что хотя бы одно событие из полной группы обязательно произойдет.
Примечание: часто полную группу событий нужно дополнять событием, что ни одно из них не произойдет.
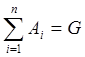
9.Противоположным событием называется такое, которое дополняет исходные события до полной группы.
Противоположное событие 
обозначает логическую связку «не» А.
С точки зрения вероятностей,
противоположное событие означает, что событие не произойдет.
10.Равновозможными
называются события, составляющие полную группу и имеющие равную вероятность
возникновения.
Такие события иногда называются
«шансами».
|
А1 |
А2 |
А3 |
|
А4 |
А5 |
А6 |
Равновозможные события лежат в основе любых азартных игр. Их равновозможность создает наибольшую неопределенность для игрока.
11.Равносильными (эквивалентными) называются события, которые при определенных условиях совпадают по смыслу, т.е. выражают одно и тоже.
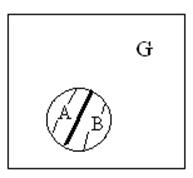
А=В
Пример: 2 промаха из 5 событий А эквивалентны 3 попаданиям.
12.Событие А влечет за собой событие В, если при возникновении события А обязательно произойдет событие В.
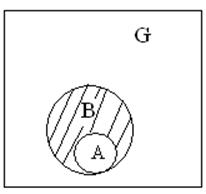
Пример: окончание института (событие А) влечет за собой окончание 2 курса (событие В).
Обратное неверно.
Примечание: А+В=В
А*В=А
Указанные соотношения между событиями показывает, что необходимо учитывать вид событий, их физическую сущность, а также необходимость того, чтобы они составляли полную группу событий.
В приведенных примерах и действиях над событиями символ вероятности опущен, однако, в реальной действительности действия выполняются не с самими событиями, а с их вероятностью.
Так, например, для полной группы событий сумма всех вероятностей будет = 1.
1.9.Следствия случайных событий для электрических цепей
Выше было показано, что можно различать принципиально 2 разных понятия, а именно сумма 2х случайных событий и произведение случайных событий. В первом случае (для суммы) это означает логическую связку «или», а во втором случае – «и».
Для технической системы означает, что существует две принципиально разных электрических цепи.
1 случай:
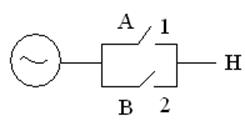
(А+В)
Событие А означает, что включен элемент 1;
Событие В означает, что включен элемент 2.
Тогда схема будет работать, если состоится событие А(1) или событие В(2), или они включены оба. Очевидно, что надежность схемы повышается, поэтому само техническое решение называется резервированным.
Итак, параллельное соединение элементов повышает надежность и определяется суммой случайных событий.
2 случай:
Элементы соединены последовательно.
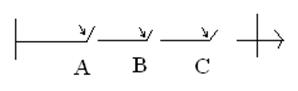
(А*В*С)
С точки зрения событий работоспособное состояние схемы тогда, когда событие А, В, С произойдут одновременно.
Итак, в этом случае работоспособность схемы из последовательных элементов определяется произведением событий. В этом случае надежность схемы по мере увеличения элементов быстро падает.
В реальной действительности мы имеем сочетания тех и других схем.
1.10.Свойства случайных событий
Случайные события по аналогии с теорией множеств обладают свойствами, значение которых позволяет рассчитать сложные технические системы.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.