Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 2

На основе этой теории Гейзенбергом был введен принцип неопределенности

,

где - некоторый импульс, получаемый электроном;

      - расстояние;

       h – постоянная Планка.

Принцип Гейзенберга гласит, если есть сила и некоторое расстояние, то, тем не менее, невозможно указать координаты электрона в пространстве состояния, иначе говоря, нельзя указать точную траекторию движения.

Таким образом, частица (электрон) не является точным определенным моментом, а является совокупностью возможностей.

Физики пришли к выводу, что эта неопределенность в положении электрона является квантовой неопределенностью, и она неуничтожима. Не зависит от точности измерений и является внутренним свойством материи. Таким образом, неопределенность является природной сущностью окружающего нас мира, ее необходимо учитывать и главным инструментом здесь выступает ТВ.

4. Неопределенность и информация

Информация как некоторое понятие также построено на вероятности. При этом по Шеннону информация есть снятая неопределенность, которая выражается через энтропию. Так, например, неопределенность снимается с помощью вопросов и ответов.

Пример: Зайдите завтра (выбор 1); зайдите во второй половине месяца (выбор 15); зайдите в следующем месяце (выбор 30).

Как видно, чем больше выбор, тем выше неопределенность. Отсюда вытекает соотношение:

I=H₀ - H_к ,

где I – информация;

      H₀ – начальная энтропия;

      H_к – конечная энтропия;

В свою очередь понятие «энтропия», которое вытекает из II начала термодинамики, приводит к хаосу (разрушению).

Н=-logP,

где Р – вероятность выбора.

Например, для алфавита из 32 букв. Н=2⁵=5 бит.

Информация на прямую связана и непосредственно определяется, как некоторая «снятая» неопределенность.

5. Неопределенность и управление

Любая техническая система используется также как объект преобразования информации.

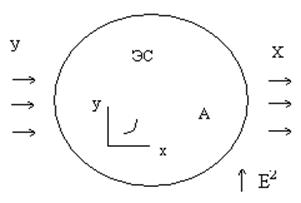
У – вектор входных возмущений;

Х – вектор отклика системы;

А – оператор преобразования;

Е – случайная помеха (белый шум)

А*Х=У

Х=А^-1*У+Е²

Таким образом, реакция системы содержит неопределенность. Задачей управления является снижение этой неопределенности и получение за счет этого качественного результата.

Почти все понятия науки об управлении кибернетикой основаны на вероятности и без ее учета реализация управления невозможна.

6. Неопределенность и игра

В практических условиях деятельности человека, он сталкивается с некоторыми обстоятельствами, которые определяются термином «игра».

Различают 2 вида:

1.  игра с соперником

Эти игры называются игры с противоположными интересами. Здесь неопределенность обусловлена интересами, способом поведения или действиями игроков, а также располагаемыми ими ресурсами (шахматы, военные сражения и др.)

Есть данные, что некоторыми полунаучными методами (подсчетом вероятности) неопределенность поведения противника учитывалась А. Македонским и Д. Донским.

Игры с противоположными интересами представляют высокую степень неопределенности, которая преодолевается с помощью ТВ.

2.  игры с природой.

В этом случае соперник, как бы не имеет своих интересов, но его реакция может быть выражена с некоторой степенью неопределенности, является недостаточно ясной для игрока. И здесь сценарий или ход событий содержит долю неопределенности.

7. Неопределенность и прогнозирование

В реальной действительности часто возникает задача прогностики, иначе говоря, прогнозирования будущего состояния технической системы или организационной системы. В этом случае автор опирается на некоторую статистику (статистический ряд) на основании которой он пытается предсказать будущее.