На первоначальном этапе закон Пуассона нашел физическое подтверждение в условиях такого физического эксперимента: во времена кавалерийских войск возникала задача о числе погибших от удара копытом, было велико, т.к. было много людей общающихся с лошадьми. Однако вероятность погибнуть от копыта бала достаточно мала, но, тем не менее, она реализовалась.
Проверка экспериментальных данных показала хорошее совпадение с законом Пуассона.
Закон Пуассона есть приблизительная запись биномиального закона распределение.
рn=С
*рm*qn-m
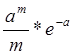
Закон Пуассона есть некоторый эквивалентный биномиальный закон, при условии, что n достаточно велико, а вероятность достаточно мала. Используя закон Пуассона можно определить также число отказов технической системы за определенный период времени.
3.8.Функция распределения СВ
Во многих случаях недостаточно иметь понятие о значении распределения СВ.
Например, для ДСВ мы не имеем всех значений случайной величины как универсального множества. Необходимо новое понятие, которое годилось бы как для ДСВ, так и НСВ.
Этому требованию соответствует понятие функции распределения.
Функция распределения СВ(Х), F(Х) определяет вероятность того, что СВ(Х) примет значение меньше чем наперед заданное значение х.
F(х)=р(Х<х)
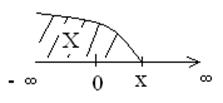
С физической точки
зрения это означает, что -
<Х<х.
F(Х) показывает вероятность того, что СВ не превзойдет наперед заданного значения х и будет находиться левее.
3.9.Свойства функции распределения
1.Функция распределения находится в интервале 0 до 1.
0<F(Х)<1
Это вытекает из того, что функция распределения есть вероятность.
Доказательство: если
Х устремить в -, то F(Х)=0, если Х
устремить в +, то F(Х)=1.
2.Функция F(Х) – есть неубывающая функция своего аргумента.
F(Х2) > F(Х1), если х2 > х1
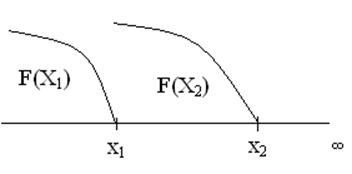
Функция распределения позволяет определить вероятность попадания СВ в некоторый интервал от a до b.
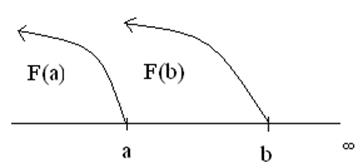
Вероятность того, что a<X<b будет F(b) – F(a)
р(a<x<b) = F(b) – F(a)
Из этого условия также видно, что
F(b)=F(a)+ р(a<x<b)
Так как вероятность величина положительная, то F(b)>F(a), что также подтверждает, что функция распределения является возрастающей функцией.
Тогда вероятность р(Х
[a;b])= F(b) – F(a)
Если устремить b к a, b>a, получим, что р(Х=а)=0
Получается, что раньше мы считали, что вероятность = 0 только в случае невозможных событий, в данном же случае события возможны и более того, оно обязательно произойдет для одной из точек. Однако, это событие является редким исключением, т.е. практически невозможным. Как же быть с теоремой сумма вероятности? Ведь сколько 0 не суммируй получится 0. На самом деле недоумение можно рассеять тем, что теорема сложных событий оперирует со счетным множеством, но не с бесконечным числом точек.
По аналогии с тем, что площадь некоторой фигуры складывается из большого числа как угодно малых площадей, но не точек(!), т.к. площадь каждой точки =0.
В связи с этим вероятность получения некоторого конкретного значения для НСВ считается =0, хотя оно и возможно теоретически.
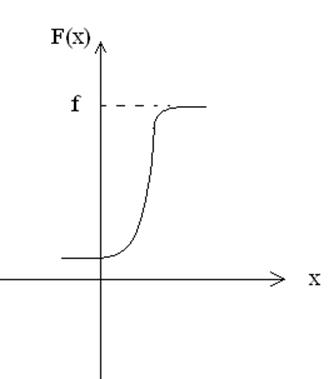
В любом случае функция распределения является возрастающей, при этом для НСВ это монотонно возрастающая функция; функция для ДСВ может иметь разрыв I рода (скачки).
3.10.Важные частные случаи
1.Выше были приведены главные рассуждения о функции распределения для НСВ.
Для ДСВ могут быть скачки этой функции (разрывы I рода)
НСВ F(Х)=р(Х<х)
ДСВ F(Х) = р(Х<х)+р(Х=хi)
|
х |
х1 |
х2 |
х3 |
|
р |
р1 |
р2 |
р3 |
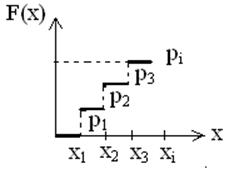
Отсюда видно, что для НСВ второй член выражения =0, т.к. вероятность для конкретных значений хi всегда =0.
В любом случае F(Х) является возрастающей величиной и при этом вероятность последовательно накапливается до 1. Вероятность куммулятивно нарастает.
2.Если СВ Х принадлежит [a;b]
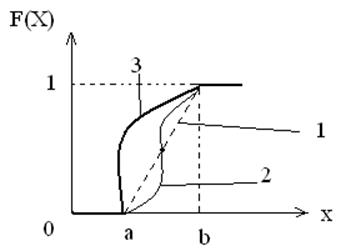
1.равномерное распределение
2.нормальное распределение
3.экспоненциальное распределение
F(X<a)=0
F(X>b)=1
3.Для функции
распределения НСВ, когда СВ Х[a,b]
можно писать:
p(a<X<b)=p(a
X<b)=p(a<Xb)=p(aXb)
Это обусловлено тем, что
p(X=a)=0
p(X=b)=0
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.