Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 13

При серьезных исследованиях, часто удается получить аналитическую форму закона распределения, то есть то или иное математическое соотношение между значениями СВ и их вероятностями.

3.3.Основные виды законов распределения для ДСВ

В настоящее время существует большое количество законов распределения для ДСВ.

Вот некоторые из них:

1.закон равномерного распределения.

2.закон геометрического распределения.

3.закон биномиального распределения.

4.закон распределения редких явлений – закон Пуассона.

3.4.Закон равномерного распределения

ДСВ Х, принимающая целочисленное значение до n, имеет равномерное распределение, если

р(Х=m)=1/n,

где m=1, 2, 3,…, n

С физической точки зрения это означает, что все случайные значения ДСВ равновозможны и имеют одинаковую вероятность.

Пример: 6-ти гранный кубик.

Х	1	2	3	4	5	6
р	1/6	1/6	1/6	1/6	1/6	1/6

 Многоугольник распределения:

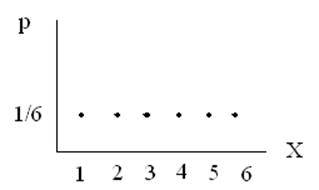
На уровне обывателя это свидетельствует о том, что «шансы» во всех случаях одинаковы.

3.5.Геометрическое распределение

ДСВ Х подчинена геометрическому распределению, если вероятность ее случайного значения определяется выражением

р(Х=m)=р*q^m-1,

где m – 1, 2, 3,…,n;

p – вероятность наступления события в единичном опыте;

q – вероятность ненаступления события в единичном опыте.

С физической точки зрения, геометрическое распределение того или иного события после некоторого количества неуспешных попыток.

Таким образом р(Х=1)=р, если первая попытка неуспешна;

р(Х=2)=р*q, если 1 неуспешная, а 2 успешная.

р(Х=m)=р*q^m-1 (m-1 попытка).

Таким образом, ДСВ Х число неуспешных попыток, предшествующих «успеху».

Геометрическое распределение представляет собой геометрическую прогрессию.

Пример: за время Т производятся попытки включить двигатель автомобиля. Каждая попытка заканчивается успехом с вероятностью 0,6 и занимает время . Определить закон распределения для времени включения двигателя (до времени запуска двигателя).

Т=Х*

Т.к. физика явления соответствует геометрическому распределению, то получим решение:

Если построить многоугольник распределения, то можно заметить, что с числом попыток вероятность запуска быстро уменьшается.

3.6.Биномиальное распределение

ДСВ Х подчиняется биномиальному распределению, если вероятность

его распределения подчинена закону:

р_m=р(Х=m)=С*р^m*q^n-m,

где m=1, 2, 3,…,n ,

р – вероятность наступления события 0р1,

q=1-р – ненаступление события.

Биномиальное распределение называется так потому, что случайные числа Х являются членами разложения бинома (р+q)ⁿ.

Биномиальное распределение отождествляется также с формулой Бернулли, в которой С есть число сочетаний.

С физической точки зрения, биномиальное распределение характеризует случай, когда части испытаний, соответствует положительный результат («успех»), а части испытаний соответствует отрицательный результат («неуспех»).

 р^m*q^n-m ,

р – число успехов, q – число неуспехов перемножают и из этого числа выбирают число сочетаний.

Эта формула соответствует идеальной модели .

В реальности р_n=С*(р^m*q^n-m) надо умножить на число сочетаний.

Биномиальное распределение является достаточно сложным, если n (число испытаний) велико, в связи с этим оно может быть несколько упрощено.

3.7.Распределение Пуассона

ДСВ Х подчиняется закону Пуассона следующего вида

р(Х=m)= ,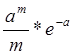

где a=m*p=const; a=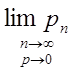 

Распределение Пуассона является более удобным для вычисления вероятности, если  , а .

Распределение Пуассона характеризует теорему образования сложной технической системы из большого числа элементов, при чем вероятность отказа (выхода из строя) этих элементов мала. Таким образом, наступление события при малой вероятности является достаточно редкой (закон редких событий).