Этот момент характеризует чувствительность среднего к отклонению больших СВ, имеющих малую вероятность.
2.Моменты центрального порядка.
Центральным моментом k-го порядка называется МО разности СВ и ее МО в k-ой степени.
для ДСВ: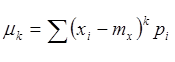 
, где i=1,2,…n
для НСВ: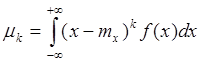 
Найдем эти моменты:
1.k=1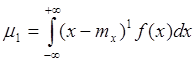 
=
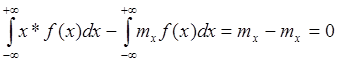
Примечание: этим доказываем еще раз 7-ое свойство МО.
2.k=2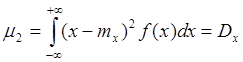 
- дисперсия.
Значит, центральный момент 2-го порядка – дисперсия.
Центральные моменты могут выражаться через начальные:
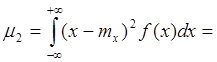
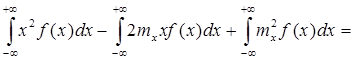
3.k=3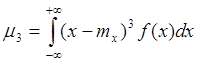 
- центральный момент 3-го порядка.
По своему физическому смыслу характеризует асимметрию закона распределения:
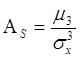
А – характеризует асимметрию; skew – косой.
Коэффициент асимметрии характеризует склонность закона распределения.
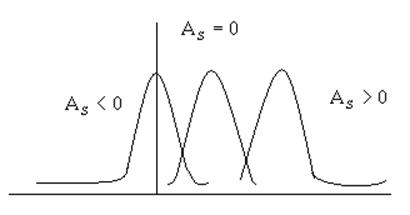
Если закон симметричен, то коэффициент =0. Если у закона правый «хвост» распределения длиннее, то коэффициент положительный; если левый – отрицательный.
Примечание: деление
на 
необходимо для того, чтобы сделать
коэффициент асимметрии безразмерным, т.к. момент 3-го порядка – величина
кубическая.
4.k=4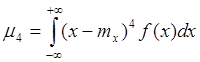 
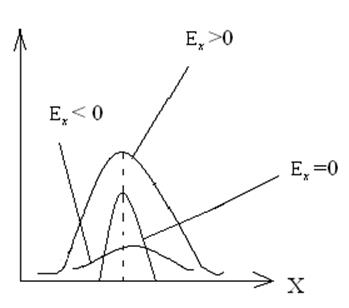
По своему физическому смыслу характеризует островершинность (уплощенность) закона распределения.
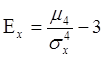
excess – излишек.
Примечание: деление
на 
необходимо потому что 
имеет размерность в 4 степени; (-3)
обусловлено тем, что для наиболее распределенного нормального закона распределения
=3.
Законы, имеющие более
острую вершину по сравнению с нормальным, имеют положительный , а имеющие меньшую островершинность
(пологость) имеют отрицательный .
Другие моменты высшего порядка физического смысла не имеют, и нами изучаться не будут.
Следует иметь в виду,
что для симметричных законов мы получили: 
, 
и все нечетные моменты =0.
3.33.Обсуждение результатов
Показано, что МО является главным центром рассеяния любой СВ относительно которого она варьирует. Термин МО следует применять вместе оба слова.
МО является критерием «справедливой» игры, т.е. МО выигрыша должно быть равно стоимости билета (входа в игру).
В соответствии с теоремой и неравенством Чебышева при любых обработках данных среднее арифметическое всегда будет стремиться к МО с увеличением числа опытов, подобно тому, как статистическая вероятность с увеличением числа опытов стремится к истинной классической вероятности.
Вследствие этого МО приобретает устойчивость и по существу становится неслучайной величиной.
Наряду с этим дисперсия характеризует рассеяние и в косвенной форме характеризует неопределенность. Чем больше дисперсия, тем больше неопределенность, тем больше риск предсказания результата и принятие правильного решения. Принято считать, что технократический взгляд всегда опирается на риск и выигрыш, а гуманистический взгляд – на безопасность.
При этом дисперсия, а в инженерных науках среднеквадратическое отклонение (СКО), отражают вариацию параметров относительно среднего. Разброс этих параметров, либо отражает случайную природу величины, либо ошибку измерений. Природное свойство любого исследователя (автора) состоит в стремлении уменьшить величину дисперсии, т.е. снизить определенность.
В настоящее время в ТВ рассматривается также лингвистическая неопределенность. Лингвистическая неопределенность обусловлена тем, что человек не читает полностью слова, а догадывается о его содержании.
midd / le – среднее
midd / ay
– полдень 
Вхо / 
qu 
В целом дисперсия характеризует число возможных исходов. Так, например, неопределенность алфавита из 32 букв равна 25 дает 5 бит. Вся неопределенность алфавита 5 бит.
Этот пример показывает, что сокращение числа исходов снижает дисперсию и неопределенность. Этому же способствует увеличение числа опытов.
Глава 4.Законы распределения (ЗР) НСВ
4.1.Общие соображения
ЗР СВ является наиболее информативной и доказательной формой представления любой СВ. Природа ЗР весьма различна.
Всего существует теоретически около 50 ЗР, но практически применяется не более 10. На основе ЗР могут быть вычислены их характеристики, включая моменты высших порядков, и в этом случае расчеты сильно упрощаются.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.