Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 15

Отсюда следует включение (невключение) концов отрезков в интервал относится к искусству автора.

4.В связи с тем, что вероятность функции распределения непрерывно возрастает, она также называется интегральным законом распределения.

3.11.Плотность распределения СВ

Выше была рассмотрена СВ Х, которая может быть построена как для НСВ, так и для ДСВ. Однако, по этой функции не всегда удобно вычислять вероятность попадания СВ в тот или иной интервал. В связи с этим вводится новая функция, которая называется плотностью распределения вероятностей (ПРВ).

ПРВ СВ – это некоторая функция f(x) представляющая собой первую производную от функции распределения.

f(x)=F^\(x)

Примечание:

1.F(x) должна быть дифференцируемая, поэтому f(x) может быть найдена только для НСВ. Ее аналогом для ДСВ является многоугольник распределения.

2.Плотность распределения представляет собой скорость изменения F(x), а именно скорость ее возрастания.

Плотность распределения в принципе характеризует вероятность попадания СВ в некоторый интервал, пусть даже бесконечно малый.

Доказательство:

Пусть заданы 2 точки

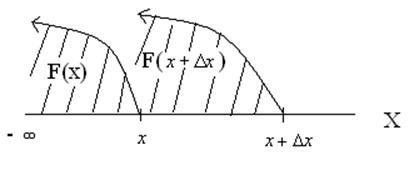
тогда вероятность попадания в интервал будет определяться пределом разности этих функций

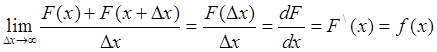
Это означает, что плотность распределения характеризует вероятность, если выполнить операцию дифференцирования, поэтому плотность распределения называют дифференциальным законом распределения.

Плотность распределения в основном опирается на понятие элемента вероятности.

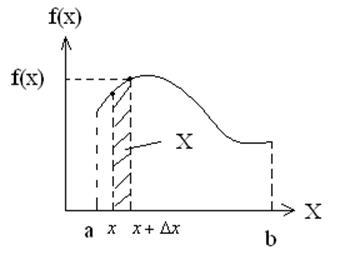
Тогда вероятность попадания в интервал

р(x<X<x+)=f(x)* =S=,

где  - элемент вероятности.

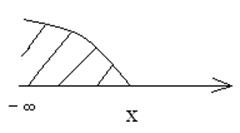
Вся площадь ограниченная f(x) характеризует вероятность попадания СВ в этот интервал (а;b),отсюда следует вероятность попадания СВ определяется вычислением площади:

р(a<X<b)=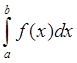

3.12.Свойства плотности распределения

1.Плотность распределения неотрицательная функция

f(x)0

То есть всегда расположена выше оси абсцисс.

Доказательство: т.к. F(x) всегда возрастающая функция, то ее производная всегда положительная.

2.Несобственный интеграл от плотности распределения в пределе от  до  равен 1.

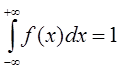
Доказательство: Площадь, ограниченная f(x) от  до  есть достоверное событие с вероятностью р=1.

3.Если СВ Х, ограниченная интервалом [a;b], то соответствующий интеграл в этих пределах тоже =1, т.к. вероятность попадания в этот интервал есть достоверное событие.

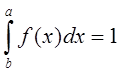
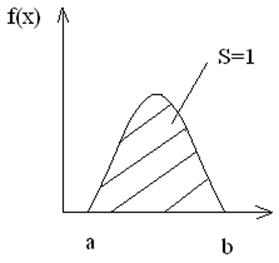
4.Если плотность распределения симметрична относительно 0

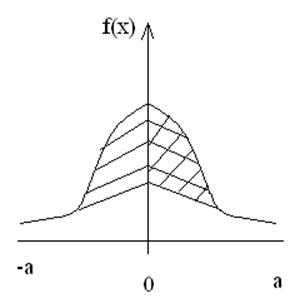
р(-а<Х<+а)=2*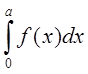

3.13.Определение функции распределения F(x) по известной плотности распределения f(x)

Выше была рассмотрена прямая задача: определение f(x) по известной F(X), как взятие первой производной.

Иногда возникает обратная задача.

Дано: f(x)

Определить: F(x)

F(x)=p()

F(x)=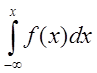

3.14.Числовые характеристики СВ

Общие соображения

Любые СВ как НСВ, так и ДСВ могут быть охарактеризованы в большинстве случаев не только законами распределения, но и также числовыми характеристиками, которые являются некоторым упрощенным эквивалентом законов распределения.

Тем не менее, в реальной действительности они имеют гораздо большее применение, чем сами законы распределения.

Различают 2 группы числовых характеристик СВ:

1.Числовые характеристики, которые характеризуют нечто среднее, а точнее средневзвешенное положение некоторого центра, относительно которого группируются другие СВ. Это среднее является некоторым положением СВ относительного которого СВ флуктуируют, т.е. отклоняются случайным образом.

К таким характеристикам положения СВ относятся: МО, мода, медиа.

2.Числовые характеристики характеризуют саму величину рассеивания относительно среднего значения, чем больше рассеивание, тем выше неопределенность.

К ним относится дисперсия, среднеквадратическое отклонение.

3.15.Математическое ожидание

Термин «математическое ожидание» (МО) возник во времена азартных игр как словосочетание «ожидание выигрыша». С приходом ТВ термин уточнился и назывался «МО выигрыша» и получил всеобщий характер и понятие выигрыша отошло на второй план.

 МО обозначается:

М[Х]=m_x=,

где М – оператор МО.

Для конкретных технических величин Х заменяется техническим параметром.

М[U]=m_u=,