Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 27

Док-во: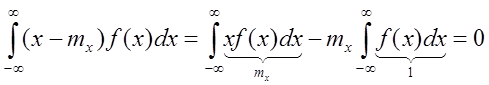

2.Ковариация 2х СВ = МО их произведения минус произведение их МО.

 

Док-во:

Таким образом, ковариация является меньшей величиной, чем M[XY].

3.Ковариация 2х СВ по абсолютной величине меньше (не превосходит) произведения СКО.

Это означает, что max ковариация достигается при значении равном произведению .

4.Ковариация СВ сама с собой равна дисперсии СВ.

для  :

Док-во:

Практическое значение этого факта трудно переоценить, т.к. во многих случаях приходится искать ковариацию СВ в квадрате.

Пример:  (1)

Этот случай представляет, что

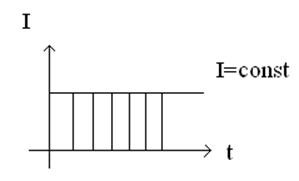
Но реальный ток флуктуирует относительно среднего значения.

Первая формула характеризует детерминистический вариант.

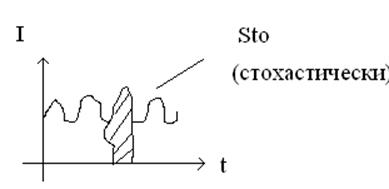
Тогда МО стохастического случая:

Т.к.

Таким образом, в реальной действительности истинные потери [Дж] всегда больше, чем они рассчитываются детерменистическим (строго причинным) методом.

5.16.Важные уточнения формул числовых характеристик

Факт зависимости СВ, если он подтверждается, позволяет уточнить формулы числовых характеристик, таким образом, что они становятся более полными , охватывающими все случаи жизни.

1.МО произведения 2-х СВ равно произведению их МО плюс ковариация (корреляционный момент) между ними.

Ранее, исходя из независимости СВ, для которых ковариация =0:

     -

это есть частный случай произведения НСВ. Вытекает из 2-го свойства ковариации.

2.Дисперсия суммы 2-х СВ равна сумме дисперсий этих величин плюс удвоенный корреляционный момент между ними.

Очевидно, что если СВ независимы, то

Док-во:

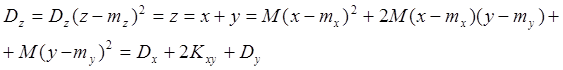
3.Дисперсия произведения  2-х СВ равна сумме дисперсий этих СВ  плюс произведение квадрата МО Х на дисперсию Y плюс произведение  квадрата МО Y на дисперсию Х.

Ранее вторые 2 члена выражения мы не учитывали, что соответствует нахождению дисперсии произведения для центрированных СВ, т.к.  и .

4.В ряде случаев необходимо писать корреляционную матрицу для 2-х или более СВ.

    обычно входит в систему линейных алгебраических уравнений.

Структура :

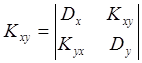
На диагонали корреляционной матрицы всегда стоят дисперсии, т.к. это есть ковариация величины самой с собой.

 - МО потери

Дисперсия дает свои потери.

Таким образом, основные числовые характеристики С 2х СВ должны учитывать фактор их зависимости или независимости.

5.17.Коэффициент корреляции

Ковариация между 2-мя СВ показывает их разброс (рассеяние, вариацию) и зависимость Х от Y. Однако размерность ковариации есть произведение размерностей СВ. В связи с этим вводится новое понятие – коэффициент корреляции, который равен:

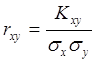
Коэффициент корреляции является безразмерной величиной и кроме того исключает вариацию (разброс) параметров относительно среднего. Таким образом, остается только фактор зависимости СВ Х и Y.

5.18.Свойства коэффициента корреляции

1. изменяется в пределах от –1 до +1

, т.к.

2.Если Х и Y независимы, то =0

Док-во: это вытекает из того, что в этом случае  .

Примечание: однако, если  отсюда не вытекает независимость СВ.

3.Если  по абсолютной величине =1, то существует жесткая функциональная связь.

    

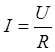
В целом  характеризует зависимость СВ, причем не любую зависимость, а только линейную зависимость.

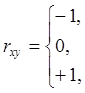                                 при

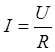
Такая функция, имеющая значение –1, 0, +, обозначается, как sign:

 (сигнум а)

 показывает только тесноту статистической линейной связи, причем жесткая функциональная связь входит, как частный случай.

  

Пример:

1.Тяга ракетного двигателя является отчасти случайной (качество топлива, технологическое отклонение). Расстояние, пройденное ракетой заодно и тоже время, также является СВ. Однако в целом, чем больше тяга, тем больше пройденное расстояние. Корреляция положительная.

2.В электрических системах токи короткого замыкания отключаются релейной защитой. Чем больше ток короткого замыкания (чем больше он превышает номинальный ток), тем больше он отключается коммутационной аппаратурой.

3.При подготовке к экзамену студент делит время на 2 части: читает лекции и смотрит телевизор. Чем больше он читает конспект, тем меньше он смотрит телевизор.