Если считать, что элемент системы или сама ТС начинает работать в момент времени t0, то время безотказной работы элемента Т является СВ, определяющей момент времени в который произойдет отказ.
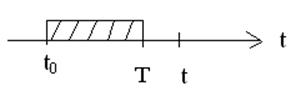
Введем некоторую
функцию надежности R(T)=p(T>t), иначе говоря, что первый отказ, определяемый Т,
произойдет позже, чем время эксплуатации t. Эта
вероятность p(T>t)=1-F(x)=1-(1-
) или
отсюда
R(T)=
Отсюда следует:
1.Время безотказной работы Т не зависит от предшествующего периода (t0). Проще говоря, отказ ТС и время наработки на отказ не зависит от того, отказывала ли система в предыдущий период или нет.
2.Если время отказа является равномерным простейшим потоком, то оно подчинено показательному ЗР.
Пример: если считать, что метеориты распределены в космосе равномерно, то количество попадания метеоритов в космическую станцию и время через которое попадет 1-ый метеорит (после начала наблюдения) никак не зависит от того, попадали ли метеориты в станцию до этого.
Таким образом, попадание метеорита в космическую станцию подчинено показательному ЗР.
4.5. Центральная предельная теорема Ляпунова
В реальной действительности на некоторое явление или процесс оказывает влияние большое число факторов. Если эти факторы случайны и каждый из них в незначительной степени влияет на конечный результат, то можно утверждать, что в итоге СВ Х, представляющая собой сумму других СВ будет распределена по некоторому общему закону – закону нормального распределения.
В общем виде закон нормального распределения определяется центральной предельной теоремой Ляпунова.
Теорема Ляпунова: если имеется достаточно большое число СВ Х1, Х2,… Хi,… Хn, то распределения суммы этих СВ при условии, что ни одна из них не оказывает подавляющего влияния, распределяется как угодно близко к нормальному закону распределения. Причем, чем ближе, тем больше СВ.
Важной особенностью закона нормального распределения является то обстоятельство, что суммируемые СВ сами могут подчиняться другим разным законам распределения.
Закон нормального распределения представляет собой колоколообразную форму, которая в частности подчиняется песчинки в песочных часах
Пример: сумма электроэнергии потребляемой электрическими приемниками, если их число достаточно велико (многоквартирный дом) будет подчинено нормальному закону. Однако, если в этом доме разместить вычислительный центр по своей мощности эквивалентный большому числу квартир, то нарушится условие центральной предельной теоремы Ляпунова и вместе с этим произойдет отклонение от нормального закона распределения.
Слово «нормальный закон» не совсем удачно, но оно отражает тот факт, что любые законы, в конечном счете, стремятся к нормальному распределению,
которое является всеобщим законом распределения на Земле.
4.6. Закон нормального распределения НСВ. (ЗНР)
Выше было показано, что в соответствии с центральной предельной теоремой Ляпунова наиболее общим ЗР СВ является нормальный ЗР. Он возникает, когда число факторов, воздействующих на СВ Х достаточно велико, но при этом ни один из факторов не имеет существенного значения. Закон нормального распределения СВ определяется следующей плотностью распределения:
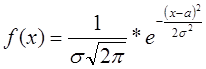
Из этого выражения ясно, что ЗНР зависит от двух
параметров:a, 
. Можно
показать, что а представляет МО, а - СКО.
; 
Док-во: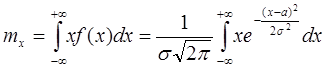 
Можно сделать подстановку:
;
;
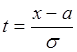Подставляя в исходное выражение, получим 2 интеграла
= 0+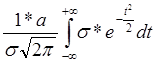
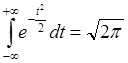называется интегралом
Пуассона.
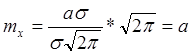
Таким образом, 
- МО.
Аналогичным образом можно показать, что представляет
собой СКО.
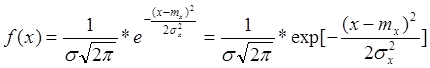
ЗНР имеет колоколообразную форму на всем интервале от
-
до +.
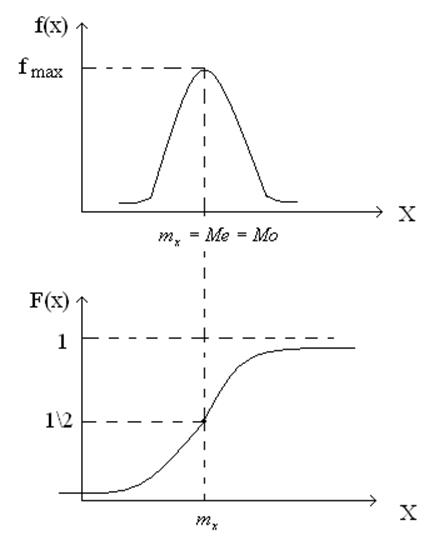
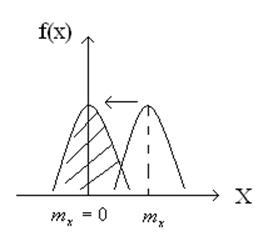
Нормированный нормальный закон совмещается своим МО с нулевой точкой (точкой отсчета).
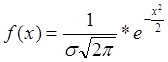
Тогда плотность нормированного распределения:
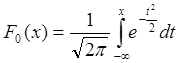
А полная функция распределения:
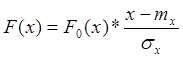
4.7.Моменты высших порядков
Плотность распределения нормального закона является симметричной , поэтому нечетные моменты высших порядков =0.
1.
2.
3.
4.
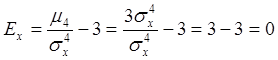
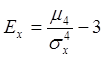
3 дописываем искусственно, чтобы Ех=0
4.8.Свойства плотности распределения ЗНР
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.