Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 4

Это определение классической «вероятности» введено Лапласом.

р(А)=,

где р(А) – вероятность наступления события А;

m – число опытов, благоприятствующих событию А;

n – число всех опытов.

Примечание: все опыты проводятся в равных условиях. Результаты опытов являются несовместными.

Частные случаи:

1.Пусть все опыты благоприятствуют наступлению события А, т.е. n=m, тогда р(А)= ==1

Такое событие называется достоверным и обозначается буквой U

р(U)=1

Достоверное событие – это событие, которое происходит всегда (неотвратимо).

Пример: восход солнца; предмет, подброшенный вверх, опускается вниз; никто не проживет 500 лет.

2.Пусть ни один из опытов не благоприятствует наступлению события А m=0,тогда р(А)= ==0

Такое событие называется невозможным и обозначается буквой V.

р(V)=0

Невозможное событие – такое событие, которое никогда не происходит и не может произойти.

Пример: изобразить число больше 1000 с помощью трех чисел; закипание воды при нормальном давление при t=10⁰С; получение оценки больше 5.

Таким образом, учитывая крайние случаи 0р(А)1. На числовой оси это означает:

              

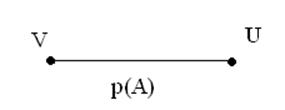
Отсюда следует, что крайние точки отрезка событий V и U не являются случайными; они либо происходят обязательно, либо нет. Поэтому достоверное и невозможное событие является строго причинным, детерминистическим.

Таким образом, классическое определение «вероятности» является исключительно простым и понятным, однако, оно предполагает, что число благоприятных опытов заранее известно.

Пример: в урне находится 6 белых и 4 черных шаров. Какова вероятность вытащить белый шар?

р(А)=60%

Примечание: по аналогии с этой задачей все задачи ТВ условно разделяются на задачи с «возвращением» и с «невозвращением» шара.

1.3.Геометрическое понятие «вероятности»

Классическое понятие «вероятности» не всегда удобно, т.к. требует равновозможности наступления событий. Иногда удобно применять геометрическое понятие

Пусть задана плоскость G и g.

 

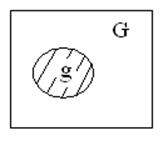
G – совокупность всех возможных элементарных исходов.

g–совокупность элементарных исходов (событий), благоприятствующих наступлению события А.

Примечание: элементарное случайное событие – неразложенный результат опыта.

Тогда, геометрическая вероятность – это результат, отношения площади g ко всей совокупности исходов G.

р(А)= мера g / мера G=mes g / mes G=S_g / S_G

Иначе говоря, геометрическая вероятность – это отношение размеров. При этом размеры могут определяться площадью, длиной или объемом.

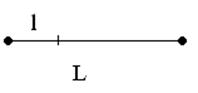  р(А)=l/L

Пример: 1.какова вероятность попадания наугад выбранной точки в круг, вписанный в квадрат радиусом R.

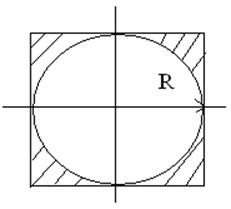
р(А)=S_круга /S_{квадрата}=пR²/4R²=п/4

2.какова вероятность попадания наугад выбранной точки в квадрат, вписанный в круг.

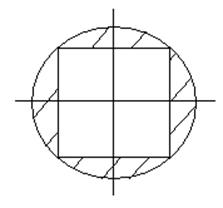
р(А)=S_{квадрата} /S_круга=2/п

3.задача о встрече.

2 студента договорились о встрече между 12 и 13 часами. При условии, что один ждет другого не более 20 минут. Какова вероятность их встречи?

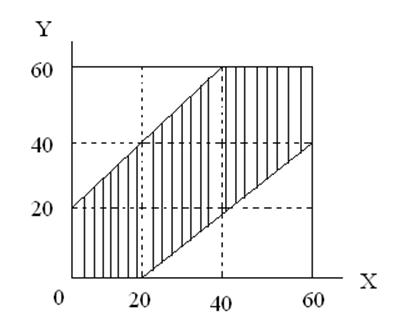
X – Y20

р(А)=S_{встречи} /S_{квадрата} =60²-40²/60²=5/9

Несмотря на большое время ожидания вероятность встречи или невстречи  50%.

4.время превышения предельного напряжения

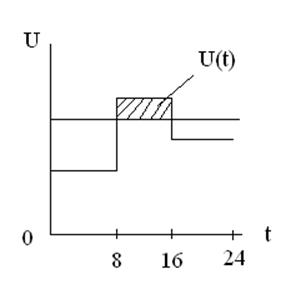
Какова вероятность того, что напряжение превысит номинальное?

р(А)=t_пр/t_{суммарн}=8/24=0,3

1.4.Статистическое понятие «вероятности»

В реальной действительности во многих случаях вероятность можно определить, как результат некоторой статистики, которая характеризует благоприятственные исходы тех или иных опытов.

Это понятие необходимо, т. к. во многих случаях априори (до опыта) нельзя сказать что-либо о вероятности наступления события.

Статистическое понятие вероятности является ключевым в инженерных дисциплинах, и оно определяется по формуле:

р(А)^*=m/n,

где m – число благоприятных событий, взятые из реальной статистики ;

n – число всех опытов.

Доказано, что при mстатистическая вероятность совпадает с классической.

lim   р(А)^*=р(А)

n

Пример: результаты бросания монет показывает

№	число опытов	герб	вероятность	автор
1	4040	2041	0,508	Бюффон
2	12000	6091	0,5016	Пирсон
3	24000	12012	0,5005	Пирсон