Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 12

1.Число пассажиров на платформе метрополитена ежедневно в 10 утра.

2.Число абонентов, соединенных АТС в течении часа.

3.Число студентов, сдавших сессию с оценкой «удовлетворительно».

Характерной чертой всех этих СВ, является то обстоятельство, что все они имеют конкретное численно изолированное значение.

Такие СВ будем называть - дискретные СВ (ДСВ).

ДСВ называется величина значение которой можно пронумеровать.

Для ДСВ  вероятность оценивается как

р(Х=х_i)=число

Наряду с этим можно наблюдать другой вид случайных величин.

Пример:

1.Абсцисса отклонения выстрела или попадания от центра (боковое уклонение).

2.Отклонение попадания снаряда до цели (недолет, перелет).

3.Отклонение амплитуды синусоидального напряжения по величине.

Характерной чертой этих примеров является, что СВ заполняют собой весь интервал возможных значений, значения примыкают к друг другу и неотделимы друг от друга (между собой).

Такие СВ будем называть - непрерывные СВ (НСВ).

Т.к. число точек на любом отрезке бесконечно, то для НСВ р(Х=х_i)=0.

Иначе говоря, вероятность того, что НСВ примет какое-то конкретное значение х_i всегда = 0. Это означает можно искать вероятность попадания СВ в некоторый интервал, пусть даже очень малый, но не само значение.

В этом конкретное отличие НСВ от ДСВ.

Аксиоматическое определение СВ таково: СВ (Х), связанное с данным опытом есть числовая функция, определенная на множестве достоверных событий.

Замечание: в практической деятельности предполагается, что автор сам определяет, является ли СВ дискретной или непрерывной и от этого зависят дальнейшие математические операции.

Примечание: в реальных исследованиях НСВ обычно измеряется дискретным образом, через некоторый интервал.

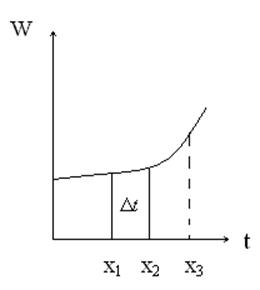
Здесь интервал квантования.

Таким образом, любая НСВ, представляющая собой аналоговый сигнал, «оцифровывается», то есть представляется набором дискретных величин. Пренебрегать или нет уровнем квантования, решает автор.

3.2. Законы распределения ДСВ

Законом распределения ДСВ называется соотношение, устанавливающее связь между возможными значениями СВ и соответствующими им вероятностями.

р_m=р(Х=х_m),

где m=1, 2, 3,…, n

Различают 3 формы представления закона распределения:

1.Ряд распределений

представляет собой некоторую таблицу в которой каждому значению СВ поставлена в соответствие его вероятность.

Х	х1	х2	хi	хn
р	р1	р2	рi	рn

Т.к. возможные значения составляют полную группу событий независимых в совокупности, то сумма:

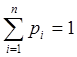
Рассмотрим закон распределения в форме ряда распределения для бросания 2-х кубиков. Если  кубики бросаются одновременно, то число набранных очков может измениться от 2-х до 12-ти.

Х	2	3	4	5	6	7	8	9	10	11	12
р	1/36	2/36	3/36	4/36	5/36	6/36	5/36	4/36	3/36	2/36	1/36

Таким образом, максимальное значение вероятности «семь очков». Ряд распределения теоретически может простираться до , если имеется счетное множество неограниченное сверху.

2.Многоугольник распределения

закон распределения СВ может быть представлен графически и является геометрическим аналогом ряда распределения.

По оси абсцисс откладываются СВ, а по оси ординат вероятности.

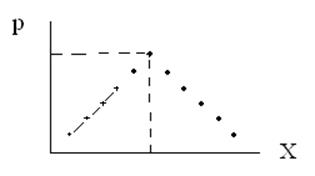
Черточки, соединяющие значения, носят эстетический характер, т.к. вероятность между конкретными числами не имеет конкретного значения.

3.Аналитическая форма закона распределения

это форма является наиболее сложной и широко применяемой. В этом случае вероятности наступления того или иного случайного значения определяется аналитическим выражением.

р(Х=х_i)=р*q^i-1

Все формы представления закона распределения являются удобным в разных случаях.

Например, при статистических обработок результатов часто имеет ряд распределения, который называется временными рядами, статистической выборкой или случайным рядом.