Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 29

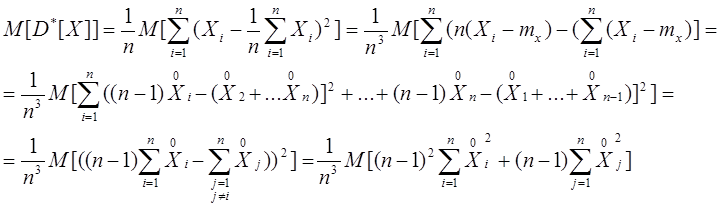
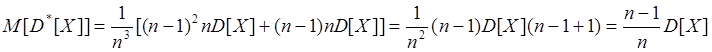
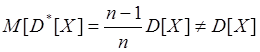
Далее обозначим:

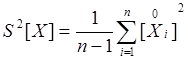
S – несмещенная оценка дисперсии СВ Х.

6.4.Интервальные оценки

Для определения интервалов оценок вводится доверительный интервал.

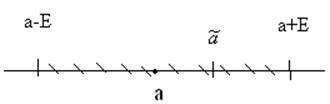
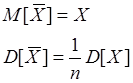
Оценка подчинена ЗР, согласно центральной предельной теоремы Ляпунова как бы ни были распределены СВ их сумма распределена по нормальному закону.

6.5.Формула Лапласа (интеграл вероятности)

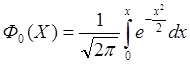
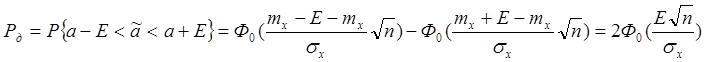
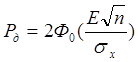
Перейдем к оценке дисперсии СВ:

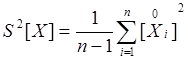
Оценка дисперсии СВ распределена по нормальному закону, т.к. сумма квадратов центральных величин распределена по биквадратному закону, а при  ЗР  к нормальному.

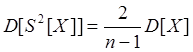
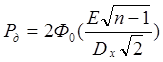
6.6.Проверка правдоподобности гипотез

Критерии значимости

          - критическая функция распределения;

- эмпирически полученная функция распределения СВ.

       - расхождение между эмпирической функцией распределения и гипотетической.

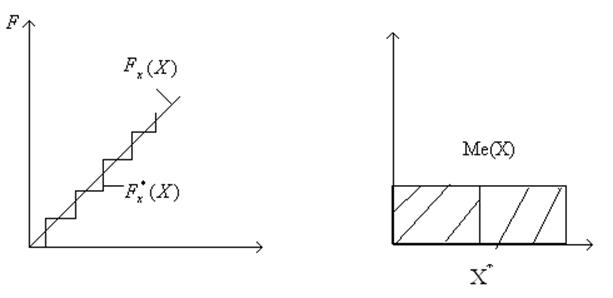
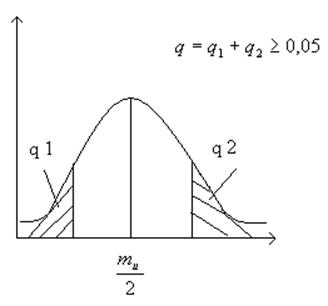
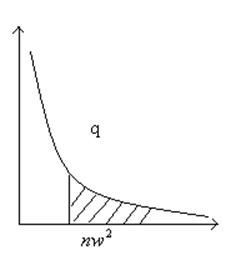
Для определения критерия значимости используется формула:

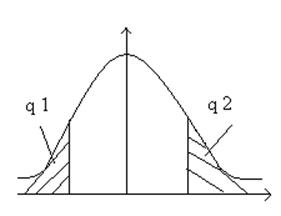
1.если q мал, то имеется опасность принятия неправильной гипотезы.

2.если q велик, то имеется опасность отброса правой гипотезы.

6.7.Критерий принадлежности двух выборок единой генеральной совокупности

Критерий Вилькоксона

Для использования критерий Вилькоксона прежде всего необходимо составить единый вариационный ряд из 2-х выборок  и . Перемешанный по признаку возрастания элементов выборок. Критерием согласия гипотезы о принадлежности двух выборок единой генеральной совокупности служат числа инверсий  и  характеризуется степень перемешанности вариационного ряда.

Пример: пусть имеется выборка Х, состоящая из двух элементов  и .

Составляем вариационный ряд по возрастанию: .

Составляем сочетание инверсий :

,

n – число выборки Х,

m – число выборки Y.

12+8=4*5

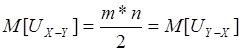
Гипотеза о принадлежности 2-х выборок генеральной совокупности не противоречит располагаемому статистическому материалу с уравнением значимости равным:

,

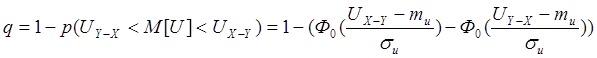где Ф₀ – функция Лапласа

6.8.Критерий равенства МО

Критерий равенства МО очень удобен для оценки правдоподобности гипотезы о принадлежности двух выборок единой генеральной совокупности при наличии лишь объемов выборок n и m и статистических оценок их МО и дисперсий.

Имеется:

Вводим оценку СВ :

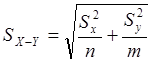
Подстановкой СВ  обозначим:

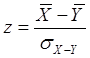
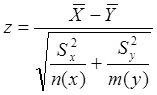
СВ z при справедливости гипотезы о принадлежности двух выборок единой генеральной совокупности распределена по нормальному закону с параметрами:

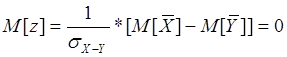
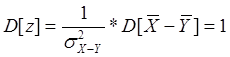
Вероятность попадания и удовлетворения гипотезы при распределении по нормальному закону:

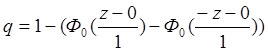
6.9.Критерий равенства дисперсий

(Критерий Фишера)

Использование критерий Фишера предполагает наличие известных объемов выборок. Суть критерия Фишера заключается в том, что производится проверка значимости различия оценок двух дисперсий  и .

большая из оценок  и ;

меньшая  из оценок  и .

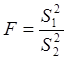
Уровень значимости гипотезы о равенстве дисперсий двух выборок определяется:

,

где  - функция распределения СВ со степенями свободы .

;

,

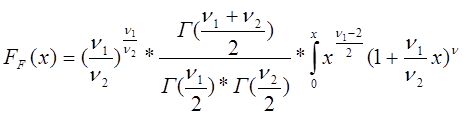где Г - гамма-функция.

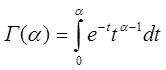
6.10.Проверка гипотез о виде закона распределения СВ

Критерий Пирсона ()

При использовании критерия согласия Пирсона необходимо весь диапазон значений объединенной выборки z разбить на интервал

 ; i=1…k

;

и определяем число m_i членов выборки попадающих в данный интервал i.

При гипотетическом нормальном законе распределения справедливо:

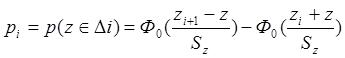
Результаты предварительных вычислений при применении критерия  Пирсона представлены в табличной форме:

	Разряд		…
			…
			…
		…	…	0,5
		-0,5	…	…
			…
		…	…	…

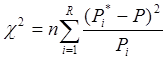
6.11.Критерий Мизеса ()

Этот критерий основан на рассматривании отклонений статистической функции распределения для каждого члена выборки z по от соответствующих значений гипотетической функции распределения.

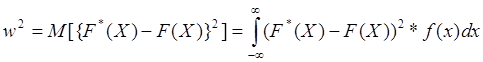
Предполагается, что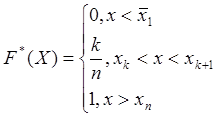

Тогда :

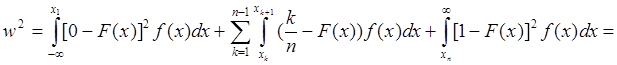
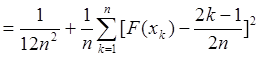
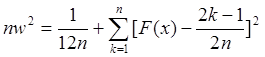
Зависимость уравнения значимости правдоподобности гипотезы о виде ЗР от величины расчетного критерия  рассчитывается таблично.

гипотеза противоречит закону о нормальном распределении.