5.9.Зависимые и независимые СВ
СВ Х и Y, входящие в С 2х СВ могут быть как зависимые, так и независимые, т.е. влияет ли одна из них на вероятность значения другой. По теореме умножения для случайного события было показано:
р(АВ)=р(А)*р(В)
При этом условная вероятность СВ равна безусловной вероятности СВ:
р(А)=р(А/В); р(В)=р(В/А)
По аналогии с этим доказательством можно считать, что СВ входящие в 2-мерный случайный вектор будут независимы, если совместная плотность распределения:
![]()
Для НС компонентов вектора XY совместная плотность распределения f(x,y) равна произведению частных одномерных плотностей.
Это условие является необходимым и достаточным. Соответственно из этого вытекает (см формулу с *), что
![]() ;
; ![]()
Свойство зависимости и независимости СВ X и Y является взаимным, если Х не зависит от Y, то и Y не зависит от Х.
Свойство зависимости и независимости СВ шире понятия функциональной зависимости, т.к. охватывает случай неявной вероятностной зависимости.
5.10.Числовые характеристики С 2х СВ
Как и для одномерного случая нахождение числовых характеристик, они могут быть определены и для С 2х СВ. Это целесообразно делать в связи с тем, что работа с ЗР СВ (и тем более 2-мерных) является достаточно сложной и трудоемкой работой.
Как и ранее для С 2х СВ могут быть найдены МО 2-мерного случайного вектора и дисперсия, характеризующая отклонение СВ от центра рассеяния. По аналогии с одномерными СВ для 2-мерных СВ в случае ДСВ берется сумма, а для НСВ сумма заменяется интегрированием. Отличие состоит в том, что для ДСВ берется двойная сумма, а для НСВ – двойной интеграл. Для МО следует использовать следующее выражение:
для
ДСВ: 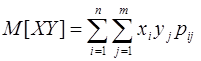 ,
,
где ![]()
для НСВ:
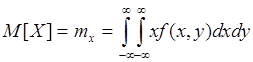
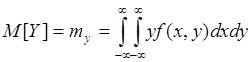
Примечание: для
одномерной функции было: 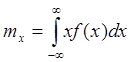
Таким образом, для С 2х СВ МО отличается тем, что подставляется совместная плотность распределения и выполняется операция двойного интегрирования.
Для дисперсии выражение имеет вид:
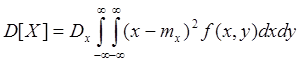
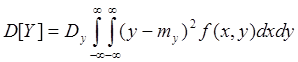
Можно воспользоваться также формулой:
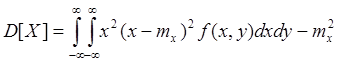
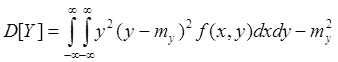
Примечание: было ![]()
В ряде случаев необходимо искать МО условной плотности распределения в частности МО одной СВ при изменении другой.

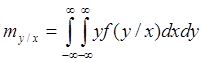
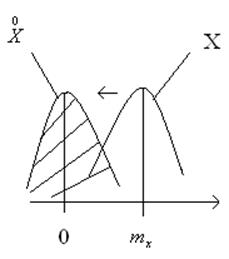
Формулы показывают на сколько изменится МО СВ X или Y при изменении другого аргумента Y или Х . Однако этих числовых характеристик для С 2х СВ оказывается недостаточно, т.к. возникает интерес к статистической связи между СВ.
5.11.Корреляция 2х СВ
В настоящее время общепризнанно, что статистическая связь между некоторыми величинами является более широким и важным понятием, чем функциональная связь. Т.к. жесткая функциональная связь является частным случаем статистической связи при жесткой корреляции между 2-мя СВ.
Корреляционная связь характеризует влияние СВ друг на друга в статистическом смысле. Введем понятие ковариация или корреляционный момент. В этом термине вариация означает случайное отклонение СВ от ее МО, т.е. разброс (флуктуация).
Со – совместное влияние или совместное отклонение. (Со - Chairman).
В русской интерпретации переводится как «со» (согласование, соавтор, сопредседатель). Таким образом, слово ковариация – совместное отклонение и влияние.
Ковариация (корреляционный момент) есть МО произведения отклонений СВ Х и Y от их МО.
![]() ,
,
где ![]() - центрированные значения.
- центрированные значения.
Примечание:
Каково МО центрированной величины СВ?
![]()
Следует иметь ввиду, что корреляционный момент:
![]()
Ковариация между X иY равна ковариации между Y и X (коммутативная операция).
Ковариация может быть вычислена как для ДСВ, так и для НСВ:
для
ДСВ: 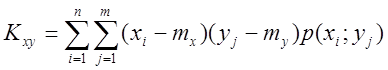
![]() означает
означает ![]()
для
НСВ: 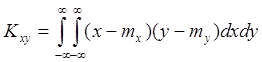
Ковариация имеет размерность произведения 2х СВ и характеризует как зависимость СВ друг от друга, так и величину их рассеивания (разброс).
5.12.Свойства ковариации
1.Ковариация 2х НСВ равна нулю. Это правило означает, что из независимости СВ вытекает их некоррелярированность, обратное неверно.
![]()
Док-во: ![]() (см. предыдущую лекцию).
(см. предыдущую лекцию).
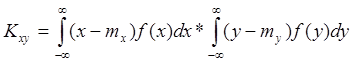
Каждый из этих интегралов =0, т.к. является первым начальным моментом.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.