Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 10

4.Если В влечет за собой А. то влечет ли за собой ?

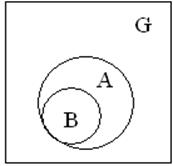
Ответ: нет.

Правильный ответ:

Пример: Событие А – попадание 1 раз из 2-х выстрелов; событие В - попадание 2 раза из 2-х выстрелов.

означало бы, что попаданий 1. Означает ли это. что 1 выстрел будет промах? ()

Ответ: нет.

5.Для 3-х параллельно соединенных попарно элементов:

(А+В)*(В+С)*(А+С)=А*В+В*С+А*С

6.Независимость и зависимость событий возникает в следующем случае: если события несовместны, то они зависимы (см. теорему), потому что появление одного из них делает вероятность появления другого = 0.

7.События, представляющие собой полную группу событий, являются зависимыми. Так непоявление ни одного из них делает вероятность появления последнего = 1.

8.Равновозможные события могут быть как независимые, так и зависимые.

2.10.Применение алгебры событий для оценки надежности электрических схем

№	схема	А - включение	В - выключение
1		А1	В1
2		А1*А2	В1+В2
3		А1+ А2	В1*В2
4		(А1+ А2)*А3	В1*В2+В3
5		А1* А3+ А2*А4	(В1+В3)*(В2+В4)
6		(А1+А2)*(А3+А4)	В1*В2+В3*В4

Примечание: вышеприведенное выражение «вкл-выкл» основаны на теореме двойственности: сумма прямых событий = произведению противоположных.

2.На самом деле мы имеем дело не с событиями, а с их вероятностями.

3.Указанные формулы должны быть записаны более точно с учетом того, совместны события или нет, а также зависимы события или нет.

2.11.Вероятность появления хотя бы одного события

На практике часто случаются случаи, когда нужно определить вероятность того, что произойдет хотя бы одно событие. Это условие определяется следующей теоремой.

Теорема: вероятность появления хотя бы одного из событий А₁, А₂,…,А_n независимых, в совокупности, равна разности между 1 и произведением вероятностей противоположных событий.

р(А)=1-q₁*q₂*…*q_n

q₁=1-р(А₁)=р(₁)

q₂=1-р(А₂)=р(₂)

…

q_n=1-р(А_n)=р(_n)

q – вероятность того, что событие не произойдет.

р+q=1

р(А)+р()=1

В частном случае, когда вероятность наступления событий одинаково, формула преобразования вида:

р(А)=1-qⁿ,

где n – число событий в совокупности.

Пример: вероятность сдать экзамен студентом, который знает 40% материала р(А)=0,4.

Сколько должен сдавать экзамен, чтобы с вероятностью0,9 он сдал его хотя бы 1 раз. Будем считать, что при n  попытках экзамен будет сдан, т.е. событие хотя бы 1 раз произойдет; будем также считать, что события независимы в совокупности, тогда

р(А)=0,4

q(А)=1-0,4=0,6

1-0,6ⁿ 0,9

0,6ⁿ 0,1

n=log 0,1/log 0,6=4,85

Итак, n>3, что недопустимо.

Вероятность того, что студент сдаст экзамен 1 раз из 3-х испытаний n=3 р(А)=0,936. с какой вероятностью событие появится один раз в одном испытании?

0,936=q³,

тогда q=0,4, значит р(А)=0,6.

Значит, вероятность сдать хотя бы один раз составляет 60%.

Примечание: следует всегда помнить, что когда требуется найти вероятность появления хотя бы одного из совместных событий А₁, А₂,…,А_n всегда проще найти вероятность противоположных событий и затем вычесть их произведение из 1.

р(А₁+А₂+…+А_n)=1-р()

Эта формула является изящным решением не только для совместных, но и для несовместных событий. Появление хотя бы одного события означает, что событие может появиться не только в первом испытании.

Аналогично может быть определена условная вероятность:

р(А/В)=1-р(/В)

2.12.Формула полной вероятности

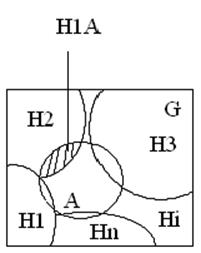
Для этих случаев наступление какого-либо события связано с наступлением другого события, что делает их связь через условную вероятность. Пусть имеется группа случайных событий – гипотез Н₁,Н₂,…,Н_n, которые составляют полную группу событий, т.е.

Н₁+ Н₂+…+ Н_n =U

Иначе говоря, какая-либо гипотеза да состоится, т.е. одна из гипотез обязательно реализуется, т.к. случайные события несовместны, то их

Н_i+H_j=V=0

на диаграмме Венна