Как видим, при
увеличении числа бросаний р(А)*
р(А),
которое можно найти априори.
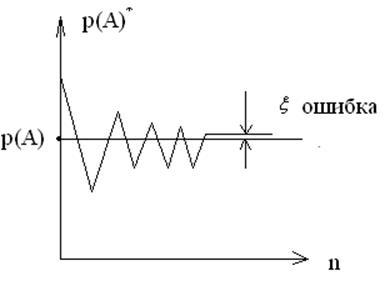
По мере увеличения n
статистическая ошибка между классической и статистической вероятностями (
) уменьшается. Отсюда следует, чем больше
опытов, тем более достоверной является найденная вероятность.
Таким образом, существует 3 определения вероятности:
1.Классическое.
2.Геометрическое.
3.Статистическое.
Каждое из них должно определятся в зависимости от исходных данных.
1.5.Вероятность и комбинаторика
В реальной действительности существует некоторое построение, обстоятельство и задача выбора, когда приходится иметь дело с некоторыми комбинациями.
В частности, это вероятностные игры. В этом случае обычно ставится в соответствие некоторому выигрышу определенная комбинация чисел.
Область математики, занимающаяся комбинациями, называется комбинаторикой.
1.6.Применение вероятностных оценок
Существует 3 вида комбинации:
1.Перестановки – комбинации, отличающиеся перестановкой элементов.
Перестановки подразумевают, что n малых элементов меняются местами, но число n остается неизменным.
Рn=n!,
где ! – произведение последовательных натуральных чисел.
Доказательство:
|
А |
n=1 |
А |
1!=1 |
|
А и В |
n=2 |
АВ, ВА |
2!=1*2=2 |
|
А,В и С |
n=3 |
АВС, СВА, АСВ, САВ, ВАС, ВСА |
3!=1*2*3=6 |
Примечание: 1.в общем случае n!=n*(n-1)!
2.0!=1
2.Сочетания – это комбинации из n элементов по m, отличающиеся содержанием.
C
=n!/m!(n-m)!
Пример сочетаний: спортлото. Нас интересуют только цифры, но не их порядок.
3.Размещения – комбинации, отличающиеся не только содержанием, но и порядком элементов.
А=n!/(n-m)!
Размещение больше на величину перестановок m элементов.
А=m!*C
Примеры размещений: азбука Морзе, сигнальные флажки на кораблях.
Если размещение допускает повторения, то формула:
=nm
1.7.Дополнительные правила комбинаторики
Правило суммы:
Если из некоторой совокупности объектов объект А может быть выбран n способами, а объект В – m способами, то либо А, либо В могут быть выбраны m+n способами
Правило умножения:
Если из некоторой совокупности объектов объект А может быть выбран n способами, а после этого объект В может быть выбран m способами, то пара этих объектов (в таком же порядке) может быть выбрана m*n способами.
1.Автомобильный номер состоит из 3х букв и 3 цифр. Пусть могут быть использованы 25 букв и 10 цифр. Какое количество номеров можно составить, используя эти комбинации из букв и цифр?
2. В русском лото можно выиграть, обозначив композицию из 5 цифр из 90 возможных. Какова вероятность выигрыша.
3. Посчитать тоже самое для спортлото 6 из 45.
4. 100 зерен помечены чернилами и брошены в кучу зерна. Зерно перемешивается. Кружкой выбирается 100 зерен. Из них 20 оказываются помеченные чернилами. Сколько зерен в куче?
5. Определить число соловьев в роще. Вылавливается 10 соловьев, помеченных. Через некоторое время вылавливается 5 соловьев, из них 2 с кольцами.
1.8.Классификация и соотношение случайных событий
Случайные события являются результатом некоторого эксперимента. Наряду с этим введем понятие элементарного события. Элементарное событие – некоторый неразложимый результат опыта, называемый также исходным.
Пример события: вероятность того, что на кубике выпадет больше 4 очков - разложимый результат. Элементарное событие – выпадет 3 очка.
События и их соотношения удобно рассматривать с помощью диаграмм Венна.
1.
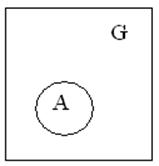
Здесь G пространство всех элементарных событий с исходами (g1, g2, g3,…,gi,…,gn)
А – событие, которому благоприятствует некоторое исходов m.
р(А)=А/G
2.Суммой двух событий А и В является событие, входящее либо в А, либо в В, либо в А и В одновременно.
,
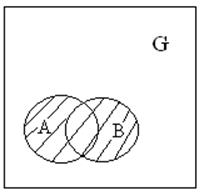
где 
- объединение из теории множеств; в ТВ - сумма.
Примечание: сумма соответствует
логической связке «или».
3.Произведением двух событий
А и В называется событие, состоящее из области в которую входят событие А и
событие В.
,
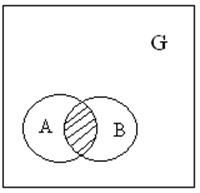
где 
-
пересечение.
Примечание: произведение
соответствует логической связке «и».
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.