Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 24

Из примера следует, что в общем случае всегда можно найти ЗР для каждой случайной составляющей вектора в общем случае n-мерного.

5.3.Функция распределения С 2х СВ

Как известно для одномерных СВ удобным средством нахождения вероятности является функция распределения – интегральный ЗР.

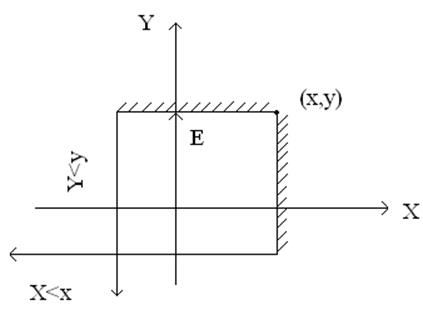
Геометрически функцию распределения для С 2х СВ можно представить с помощью случайной точки (X,Y) на плоскости ХОY с координатами (x,y).

F(x)=p(X<x)

Можно констатировать, что случайной точкой (х, у) ограничивается некоторый квадрант на плоскости, который можно обозначить, как Е. Тогда можно дать следующее определение 2-мерной функции.

Функция распределения 2-мерной СВ F(x, y) есть вероятность совместного выполнения 2-х неравенств X<x и Y<y.

F(x, y)=p(X<x, Y<y)=p(XYE)

Иначе говоря, это означает, что любая точка 2-мерного случайного вектора будет находиться левее и ниже границ области Е, очерченная координатами (х, у). При этом в декартовой системе координат это есть некоторые векторы, расположенные ортогонально.

Примечание: в принципе эта точка может быть задана вектором в полярной системе координат, но мы не будем этого делать.

5.4. Свойства функции распределения 2-мерной СВ

Эти свойства в значительной степени сходны со свойствами одномерной функции распределения. Однако имеют свои особенности, т.к. требуют соблюдения двух условий по Х и по Y.

1.Функция распределения F(x, y) является положительной величиной или равной 0 и находится в пределах от 0 до 1.

Док-во: свойство вытекает из самого понятия вероятности.

2. Функция распределения F(x, y) есть неубывающая функция каждого из своих аргументов.

 при х₂>х₁

 при у₂>у₁

Док-во: увеличение того или иного аргумента или их обоих ведет к увеличению области ее и , следовательно, к увеличению вероятности.

При сдвиге границы по х вправо, вероятность попасть случайной точкой левее Х увеличивается.

Аналогичное рассуждение верно для у только граница смещается вверх.

3. Существует ряд предельных соотношений для 2-мерной СВ.

3.1.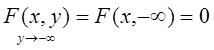

Док-во: событие Y<- является невозможным и вероятность функции =0.

3.2.

3.3.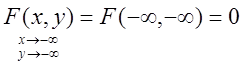

Квадрант Е сжимается до одной точки.

3.4.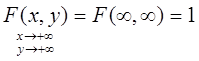

Док-во: при сдвиге границ вправо до бесконечности и вверх до бесконечности квадрант Е занимает всю плотность, и вероятность попадания в него является достоверным событием (U).

4.При изменении одного из аргумента, безразлично какого до бесконечности двумерная плотность распределения вырождается в частную функцию распределения (одномерную) противоположного аргумента.

Это означает, что функция распределения СВ Х или Y от случайного аргумента х или у является функцией только одного аргумента.

Док-во: если один из аргументов увеличить до , то условие X<x или Y<y становится достоверным событием, а любое событие совместно с достоверным событием имеет вероятность самого события.

Этими выражениями показано, что 2-мерная функция распределения может быть представлена 2-мя одномерными функциями распределения .

5.5.Вероятность попадания СВ в прямоугольник

На практике часто возникает необходимость определения вероятности попадания случайной точки (х, у), о которой мы говорили в некоторую область.

Рассмотрим в начале достаточно простой случай, когда геометрическая фигура представляет собой прямоугольник.

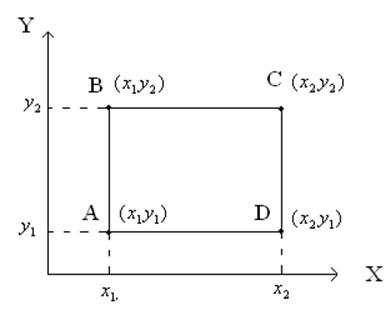
Вероятность попадания случайно выбранной точки будет определяться 2-мерной функцией распределения, равной вероятности того, что

Эта вероятность может быть найдена следующим образом: сначала вычислить вероятность попадания в полосу ВС, а потом из нее вычесть вероятность попадания в полосу АD.

В общем случае, если геометрическая фигура имеет сложную форму, то приходится прибегать к двойному интегрированию.

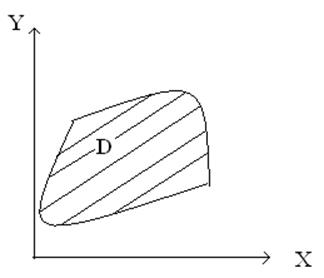
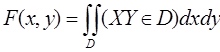
Таким образом, вероятность попадания точки в некоторую область зависит от геометрических размеров этой области.

Очевидно, что при стягивании этой области в точку, вероятность попадания =0.

5.6.Плотность распределения вероятности 2-мерной СВ