Наряду с этим, чем больше он читает
конспект, тем лучше он сдает экзамен. Корреляция положительная. Т.е. одна и та
же СВ может иметь разную корреляцию.
5.19.Зависимость
СВ и корреляция
Доказано, что для НСВ
корреляция =0. Однако если корреляция существует, то СВ могут быть как
зависимыми. так и независимыми. При этом, если 
, то это
означает не независимость, а характеризует отсутствие линейной связи.
Существует важное исключение: для нормально распределенных СВ независимость означает некоррелированность , а отсутствие корреляции означает независимость.
Таким образом, понятия зависимости и независимости, коррелированности и некоррелированности не являются тождественными в общем случае, кроме случаев с нормальным законом распределения.
5.20.Линия регрессии
Часто чтобы подчеркнуть тенденцию статистической зависимости строятся кривые/прямые линии регрессии.
Регрессией называют зависимость МО первой СВ от случайных значений другой СВ.
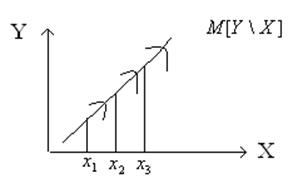
Линия регрессии означает, что при некотором значении одной СВ можно найти распределение другой СВ. Если СВ коррелированны, то линии регрессии пересекаются под некоторым углом.
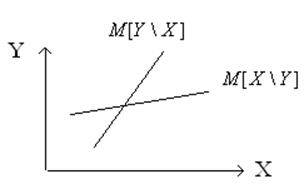
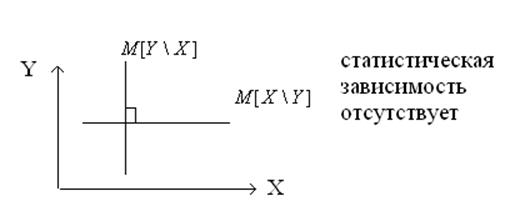
Иногда линию регрессии можно построить оптимистичным образом минимизируя квадраты отклонения.
Тогда получается линия средней квадратической регрессии, которая находится методом наименьших квадратов.
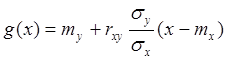
Линия средней квадратической регрессии находится в математической статистике.
5.21.Обсуждение результатов
Выше было показано, что ТВ не смотря на кажущуюся размытость результатов, позволяет получать весьма важные и точные оценки, которые незаменимы и не могут быть превзойденными во всех дисциплинах требующих принятия решений в условиях неопределенности.
ТВ дает более широкие численные оценки, нежели детерминистический подход (строго причинный). При этом последние являются частным случаем вероятностной теории. В настоящее время общепризнанно, что любые численные оценки без доверительных интервалов и вероятности их получения мало чего стоят. Теперь только «плохие» люди не сопровождают численные оценки вероятностью их наступления.
Глава 6. Математическая статистика
6.1.Основные положения
Математическая статистика (МС) – раздел ТВ предметом, которой является разработка методов регистрации, описания и анализа результатов эксперимента по наблюдению над случайными массовыми процессами.
Выборка – часть генеральной совокупности, изъятая для статистического изучения.
Генеральная совокупность – идеализация реальной совокупности (теоретически бесконечная) из которой производится выборка конечного объема для статистического изучения величины как случайной.
Задачи МС:
1.Определение законов распределения СВ (равномерный ЗР, нормальный ЗР, усеченный ЗР, экспоненциальный ЗР).
2.Определение оценок числовых характеристик СВ (МО, дисперсия, мода, медиана).
3.Проверка правдоподобности гипотез (по критериям значимости, по критерию принадлежности 2-х выборок одной генеральной совокупности) и о виде ЗР.
4.Задача прогнозирования.
Требования к выборке:
1.Выборка должна иметь достаточный объем.
2.Выборка должна быть репрезентативна (должна быть обеспечена независимость испытаний, а также случайность обеспечения экспериментом).
6.2.Статистические функции распределения
при этом
,
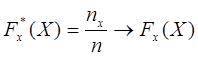где n – число опытов
nx – число опытов при которых произошло событие Х.
По теореме Чебышева:
,
где 
- малые величины.
Разность между
оценкой функции распределения СВ и самой функцией меньше по модулю Е с
вероятностью больше 
, где - малые
величины, с учетом данного выражения:
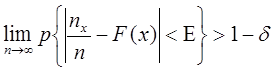
6.3.Оценка числовых характеристик СВ
Характеристики положения
В данном случае будут
рассмотрены ДСВ, точечные оценки этих величин могут иметь Х: 
.
Требования к оценкам числовых характеристик:
1.Состояние (при
объеме выборки, стремящемся к бесконечности, 
(оценка
СВ 
СВ).
2.Несмещенность (МО оценки СВ стремится к СВ при объеме выборки, стремящемся к бесконечности).
Пример:
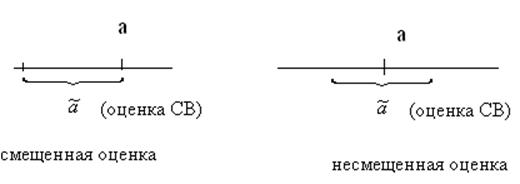
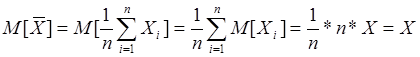
МО стремится к самой СВ.
3.Эффективность (дисперсия оценки СВ стремится к min)
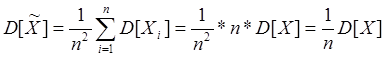
Рассмотрим это утверждение:
Док-во:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.