Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 23

Такие условия называются системой (комплексом) 2х СВ. Таким 2-мерным СВ будет посвящена эта глава.

Пример№1: производится выстрел из оружия, точка попадания снаряда может быть охарактеризована С 2х СВ.

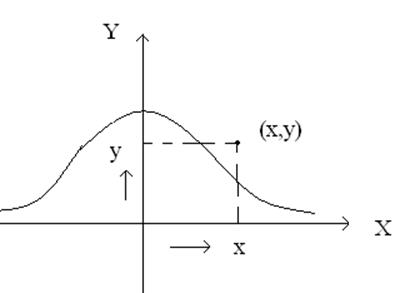
Х – отклонение по дальности;

Y – боковое отклонение (уклонение).

Тогда С 2х СВ (х,у)=р(Х=х, У=у)

Чем вызваны эти отклонения? Ответ на этот вопрос не более чем кокетство, ибо известно, многочисленными малозаметными причинами это обусловлено, которые в общем случае подчиняются нормальному ЗР. Что касается точности наведения на цель, та ошибка может выражаться в виде систематической ошибки. Эта ошибка  может быть убрана путем регулирования прицела.

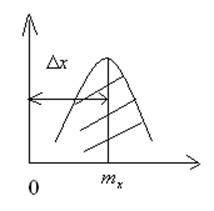
Пример№2

При синусоидальном напряжении в электрических и радиотехнических целях, С 2х СВ определяется СВ  Х – фазы включения и У – отклонение амплитуды синусоиды.

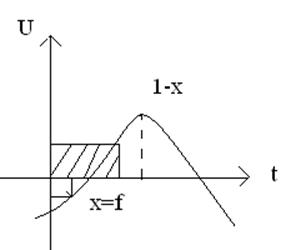
Случайные колебания амплитуды, подчиняющиеся нормальному закону, называются «белым шумом».

Пример№3: потребление электрической нагрузкой активной и реактивной мощности также представляют собой С 2х СВ = (P,Q).

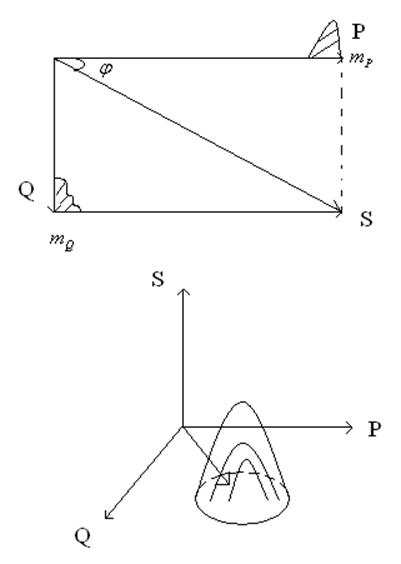
В случае системы декартовых координат система СВ содержит P и Q, а полярных координат С 2х СВ  содержит S – полная мощность и  - коэффициент мощности.

Таким образом, при рассмотрении 2-мерных СВ необходимо рассматривать основные понятия СВ как некоторые системы, что усложняет операции с ними. В ряде случа6ев можно констатировать, что число СВ входящих в систему может быть больше 2х.

Пример№1: результат сдачи сессии можно рассмотреть как систему 3х\4х СВ (Х – ТВ, Y – ТОЭ, Z – философия, F - гидравлика).

Пример№2: предсказание погоды представляет собой систему 4х СВ (X – температура,Y – давление, Z – скорость ветра, F - влажность).

В этом случае имеем дело с многомерными системами СВ, которые рассматривать не будем.

5.2. ЗР С 2х СВ

ЗР 2-мерной СВ называется перечень ее возможных значений и соответствующих им вероятностям, т.е. вероятностей пар чисел.

,

где =1,2,3…n

X=x₁,x₂…x_n

=1,2,3…m

Y=y₁,y₂…y_n

Иначе говоря, ЗР представляет собой матрицу или таблицу с 2-мя входами в виде СВ X и Y.

X        Y	y1	y2	…	yj	…	ym	p(x)
x1	p(x1 y1)	p(x1 y2)	…	p(x1 yj)	…	p(x1 ym)	p(x1)
x2	p(x2 y1)	p(x2 y2)	…	p(x2 yj)	…	p(x2 ym)	p(x2)
…	…	…	…	…	…	…	…
xj	p(xi y1)	p(xi y2)	…	p(xi yj)	…	p(xi ym)	p(xi)
…	…	…	…	…	…	…	…
xn	p(xn y1)	p(xn y2)	…	p(xn yj)	…	p(xn ym)	p(xn)
p(y)	p(y1)	p(y2)	…	p(yj)	…	p(ym)

Таким образом, первая строка имеет все возможные значения случайной компоненты Y при постоянном значении СВ Х, ее компоненты x₁.

Первый столбец все возможные значения СВ Х при постоянном значении первой компоненты СВ Y.

Т.к. события в компонентной строке и столбце образуют полную группу событий, и эти события несовместны, то можно воспользоваться теоремой сложения.

Эта вероятность того, что СВ примет значение p(x₁). Аналогичным образом можно вычислить вероятность любой другой компоненты, векторов X и Y. Т.к. все события представляют собой полную группу, то правило:

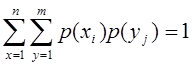
Пример: Найти законы распределения компонент случайного двумерного вектора, заданного следующим ЗР.

Частные ЗР по X и Y, компонентов вектора X Y, находящиеся суммированием соответствующих столбцов и строк.

Так по Х имеем:

 

Сумма вероятностей =1, т.к. значения Х представляют собой полную группу несовместных событий.