1. А+В=В+А свойство коммутативности для сложения
2. А*В=В*А свойство коммутативности для умножения
Примечание: свойство не применяется для матриц.
3. А*(В*С)=(А*В)*С свойство ассоциативности для умножения
4. (А+В)+С=(В+С)+А свойство ассоциативности для сложения
5. А*(В+С)=А*В+А*С свойство дистрибутивности
Также доказывается теорема двойственности де Морган:
![]() ;
; ![]()
Также доказывается следующее правило:
Продукционные правила обычно основаны на логическом «если…,то…»
Е ![]() ,
, ![]()
Домашнее задание: доказать следующие правила с помощью диаграмм Венна.
1.11.О невозможности маловероятных событий
В реальной действительности и инженерной деятельности большое значение имеет обсуждение понятий достоверное и невозможное событие.
Это обусловлено тем, что реальное положение вещей таково, что существует события, которые теоретически нельзя отнести к невозможным или достоверным, однако, вероятность появления бывает так мала, что с инженерной точки зрения они относятся к классу маловероятных событий или практически невозможных событий или почти невозможных событий.
Иначе говоря, события с исключительно малой вероятностью относятся к невозможным событиям.
Так, например, события с вероятностью 10-3 – 10-5 относятся к маловероятным. А события с вероятностью 10-6 – 10-9 относятся к практически невозможным событиям.
В связи с этим, начиная с 1 шанса на 1000 и меньше, события становятся малоосуществимы в рамках однократного опыта.
Таким образом, исключение малой вероятности в технических системах позволяют при ближайшем рассмотрении отнести многие события к практически невозможным, т.е. не учитывать их.
Глава 2 Алгебра событий
2.1.Общие соображения
Выше было показано, что события отличаются своим физическим смыслом, а также комбинациями и взаимодействием между собой. При этом необходимо выполнять над событиями определенные действия (сложение, умножение, отрицания).
Операции над событиями необходимы также для численных расчетов, определяющих вероятность наступления (ненаступления) того или иного события. Эти численные оценки крайне необходимы для расчета технических систем или инженерных конструкций.
Для проведения таких расчетов разработана алгебра событий, которая предполагает действия не с самими событиями, а с их вероятностью.
2.2.Теорема сложения для несовместных событий
Теорема: вероятность появления одного из двух несовместных событий (безразлично какого) равна сумме вероятности этих событий.
р(А+В)=р(А)+р(В)
Доказательство:
1.геометрически
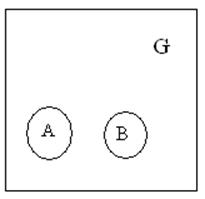
р(А+В)![]() SА+В/SG=(SA/SG) + (SB/SG)=р(А)+р(В)
SА+В/SG=(SA/SG) + (SB/SG)=р(А)+р(В)
2.аналитически
Пусть имеется число n ![]()
![]()
![]()
р(А+В)=(m+k)/n=(m/n)+(k/n)=р(А)+р(В)
Таким образом, сумма 2х событий означает, что какое-либо из событий наступит.
В общем случае теорема звучит так: вероятность появления одного из нескольких событий равна сумме вероятности этих событий.
р(А1+А2+…+Аi+…+Аn)=р(А1)+р(А2)+…+р(Аi)+…+р(Аn)
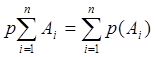
2.3.Частные случаи для этой теоремы
1.Для полной группы событий по диаграмме Венна
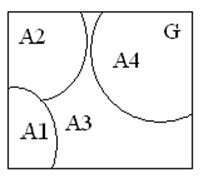
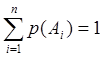 ,
,
где i=1,2,3…n
С физической точки зрения такая запись означает, что с вероятностью 1 какое-либо событие произойдет.
2.Для противоположных событий.
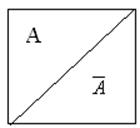
р(А)+р(![]() )=1
)=1
р(А)=1-р(![]() )=q(A)
)=q(A)
Физически это означает или прямое, или противоположное событие наступит с вероятностью 1.
2.4.Теорема сложения для двух совместных событий
Теорема: вероятность появления хотя бы одного из 2х совместных событий равно сумме вероятности этих событий без вероятности их совместного наступления.
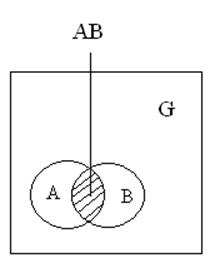
р(А+В)=р(А)+р(В)-р(АВ)
Доказательство геометрическое:
р(А+В)=(SA/SG) + (SB/SG)-(SAB/SG)
Таким образом, для совместных событий необходимо вычитать вероятность их совместного появления.
Т. к. для несовместных событий р(АВ)=V=0, то формула принимает частный вид.
р(А+В)=р(А)+р(В)
Таким образом, формула для несовместных событий является частным случаем для формулы совместных событий.
Рассмотрим формулу сложения для 3х совместных событий.
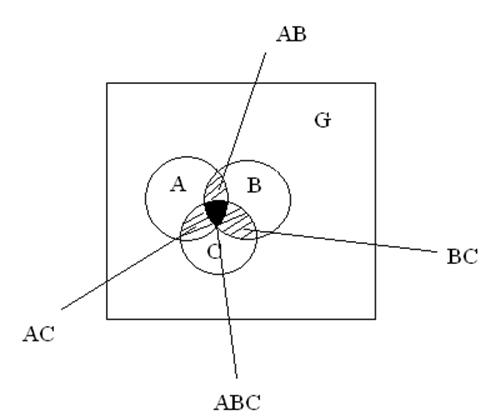
р(А+В+С)=р(А)+р(В)+р(С)-р(АВ)-р(ВС)-р(АС)+р(АВС)
Нужно прибавить р(АВС), потому что АВС вычли 3 раза.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.