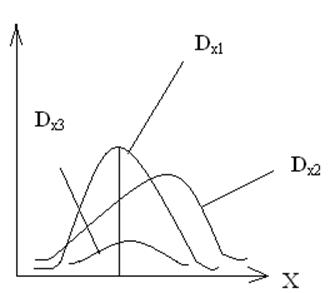
Dх1< Dх2< Dх3
Отсюда следует, что величина х3 является более неопределенная, чем величина х2.
Размерность дисперсии
определяется квадратом физической величины. Это не удобно! Поэтому в
технических дисциплинах используется другая величина – среднее квадратическое
отклонение (![]() ).
).
![]() =+
=+![]()
Теперь ![]() имеет размерность МО и физической величины
и может складываться с МО:
имеет размерность МО и физической величины
и может складываться с МО:
mx ![]() 3
3![]()
Можно показать, что в этот интервал величина попадет с вероятностью 0,997.
Для биномиального распределения:
D[X]= Dх=n*p*q
3.18.Свойства дисперсии
1.Дисперсия постоянной (неизменной) величины =0.
D[C]=0,
где С=const.
Это ясно из физического смысла дисперсии, а также вытекает из свойства дисперсии – характеризовать рассеяние.
2.Дисперсия СВ всегда не отрицательная.
D[X]![]() 0
0
Это обусловлено тем,
что дисперсия – это квадрат величины (отрицательного или положительного числа
всегда будет ![]() 0).
0).
3.Постоянная выносится за оператор дисперсии с возведением ее в квадрат.
D[C*X]=C2*D[X]
Для среднего квадратического отклонения константа выносится без возведения в квадрат, а сама константа берется по абсолютной величине.
![]() [C*X]=
[C*X]=![]() *
* ![]() [X]
[X]
4.Дисперсия произведения двух независимых СВ равна произведению их дисперсий.
D[X*Y]=D[X]*D[Y]
5.Дисперсия суммы или разности двух СВ равна сумме их дисперсий.
D[X![]() Y]=D[X] - D[Y]
Y]=D[X] - D[Y]
Док-во: D[X-Y]=D[X+(-1)*Y]=D[X]+(-1)2*D[Y]=D[X]+D[Y]
Иначе говоря, дисперсия разности СВ равна сумме их дисперсий.
6.Дисперсия СВ + const = дисперсия СВ.
D[X+С]=D[X]+D[С]=D[X],
где С – const.
Т.к. дисперсия const=0 (смотри свойство №1).
7.Дисперсия СВ равна разности между МО квадрата СВ и квадратом ее МО.
D[X]=M[X2] - m![]()
Доказательство данного равенства будет приведено ниже.
3.19.Коэффициент вариации (Кvar)
Во многих практических важных случаях представляет интерес разброса СВ к ее МО, особенно на Западе. Это отношение называется коэффициентом вариации (Кvar).
Кvar=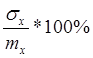
Пример: билет в лотерею стоит 50$, в одной лотерее выигрыш может составить от 0$ до 100$, в другой – от 40$ до 60$. В первом случае Кvar от 0 до 100 %, во втором случае до 20 %. Та игра в которую будет играть субъект характеризует его склонность к риску.
Тоже самое касается доходность ценных бумаг: при одной и той же средней доходности Кvar их цены может быть различен.
3.20.Среднеквадратическое отклонение (СКО) среднего арифметического при n независимых испытаниях
На практике СКО некоторого среднего от истинного МР зависит от числа опытов измерений.
СКО среднего арифметического n одинаково распределенных независимых СВ в корень квадратный из n раз меньше СКО каждой из величин.
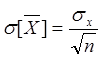
Пример: СКО (![]() ) при одном измерении некоторой длины =3м.
Пусть произведено 9 замеров, тогда
) при одном измерении некоторой длины =3м.
Пусть произведено 9 замеров, тогда ![]() =
=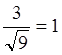 ,
значит СКО (
,
значит СКО (![]() ) составит всего 1м.
) составит всего 1м.
3.21.Квантили
Любая СВ может быть разбита на некоторые диапазоны – квантили.
Квантилем уровня q называется такое xq, при котором F(X) (функция распределения) примет значение q.
F(x)=p(X< xq)=q
Пример: пусть СВ бедности

верхний квантиль 20% характеризует число богатых и сверх богатых;
нижний квантиль 20% характеризует число бедных.
Тогда, например, медиана есть квантиль уровня 0,5. Доля xq 25% называется квартилем, 10% - децили.
В любом случае квантили является наглядным средством определения того, что СВ попадает в заданный диапазон.
3.22.Моменты высших порядков для СВ
Выше были приведены 2 основные числовые характеристики СВ. Однако они не в полной мере отражают все свойства законораспределения СВ. Для полной характеристики применяются еще моменты высших порядков, которые названы так по аналогии с механикой.
Различают 2 группы моментов высших порядков, а именно моменты начального порядка и моменты центрального порядка.
1.Момент начального порядка.
Моментом k-го порядка СВ называется МО СВ в k-ой степени.
![]()
для ДСВ: 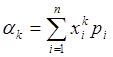 , где i=1,2,…n
, где i=1,2,…n
для НСВ: 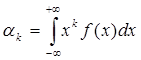
Моменты начального порядка в общем виде характеризуют центрированное положение СВ. Иначе говоря, характеризует среднее положение в более утонченном представлении.
Рассмотрим моменты начального порядка:
1.k=0 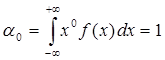
2.k=1 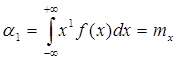
Таким образом, МО есть начальный момент 1-го порядка.
3.k=2 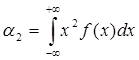
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.