Рассмотренная выше функция распределения вероятности 2-мерной СВ недостаточно в ряде случаев для определения вероятности. Другой важной характеристикой является плотность распределения 2-мерной СВ. Можно использовать термины «плотность вероятности» или «дифференциальный закон распределения».
Рассмотрим распределение плотности вероятности графически:
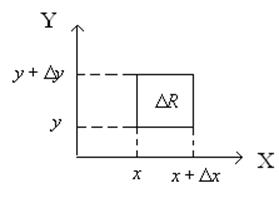
Вероятность попадания в данный квадрат 
рассматривается как вероятность попадания в
прямоугольник в предыдущем параграфе. Она будет равна:
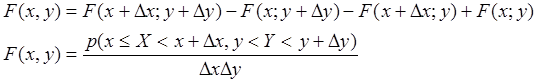
называется предел отношения вероятности попадания СВ X, Y в элементарный прямоугольный участок к площади этого участка, когда последний сжимается в точку.
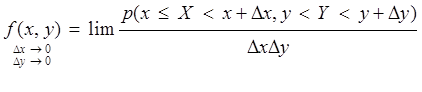
Плотность распределения как отношение вероятности к рассмотренной площади характеризует величину вероятности, приходящейся на элементарный участок.
Переходя к производным:
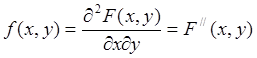
Значит, плотность распределения вероятности С 2х СВ есть вторая смешанная производная от 2-мерной функции распределения по ее аргументам х, у.
5.7.Свойства плотности распределения С 2-х СВ
1.Плотность вероятности распределения 2-мерной СВ не отрицательная функция.
f(x, y)
0
Это вытекает из того, что F(х, у) является неубывающей функцией своих аргументов (см. свойство F(х, у)).
2.Двойной несобственный интеграл с бесконечными пределами от плотности распределения вероятности =1.
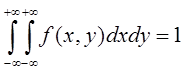
Это обусловлено тем, что объем, ограниченный плотностью вероятности определяет достоверное событие, вероятность которого =1.
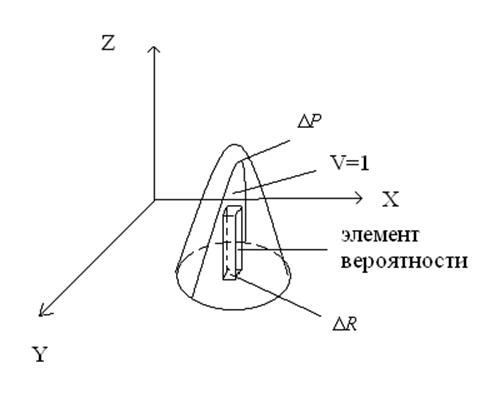
3.При ужимании
прямоугольника при 
р(Х=х, Y=y)
для НСВ =0.
По аналогии с одномерной функцией распределения вероятность попадания в точку (Х=х, Y=y) =0, хотя это событие теоретически возможно.
4.Для получения одномерной плотности распределения часто по х и у необходимо аргумент второй функции устремить в бесконечность (см. функцию распределения).
Тогда частная плотность распределения вероятности одной из СВ Х или Y есть несобственный интеграл в бесконечных пределах от 2-мерной плотности распределения по другому аргументу, тогда
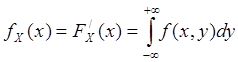
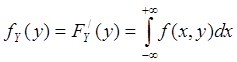
Таким образом, если известна общая плотность распределения, то могут быть найдены частные плотности распределения.
Решение обратной задачи.
Иногда требуется определить функцию распределения С 2х СВ, если известна их совместная плотность распределения.
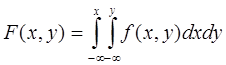
5.8.Условная плотность распределения 2-мерной СВ
Выше было показано, что если известна плотность распределения 2-мерной СВ f(x, y), то могут быть найдены частные плотности распределения одномерных СВ (см. свойство 4).
Дано: f(x, y)
Определить: 
Возникает вопрос можно ли определить совместность плотности распределения вероятности 2-мерной СВ, если известны частные одномерные плотности распределения?
Дано:
Определить: f(x, y)
Это возможно, если ввести новое понятие условной плотности распределения, подобно тому, как раньше было введено понятие условной вероятности.
р(АВ)=р(А)*р(В/А)
р(В/А)=р(АВ)/р(А)
С физической точки зрения, условная вероятность показывает как изменяется вероятность появления СВ, если другое событие произошло. Это нам как раз и нужно, где в качестве другого события выступает другая СВ.
Тогда по аналогии запишем:
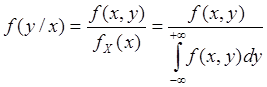
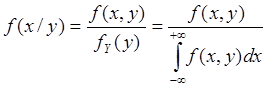
Плотность
распределения вероятностей С 2х СВ f(x, y)
равна произведению плотности вероятности одной из 2х СВ 
или
на условную плотность распределения
вероятности другой величины (f(y/x) или f(x/y)).
(*)
Условные плотности распределения играют важную роль в инженерных расчетах так, например, решение задачи позволяет перейти к одномерной функции распределения при условии, что второй аргумент принял конкретное значение.
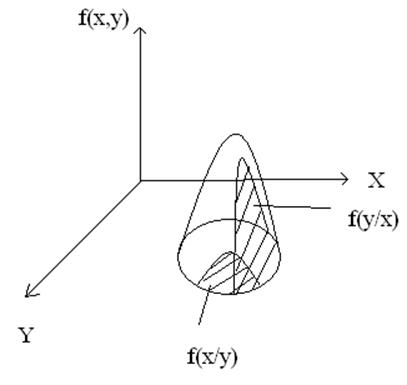
Пример: если СВ X и Y – это рост и вес человека, то они связаны случайным образом. Тогда задавшись некоторым ростом удобно рассмотреть расположение веса людей, имеющих этот рост. Верно и обратное, задавшись некоторым весом рассмотреть расположение плотности вероятности людей с данным весом.
Как видно из рисунка из 2-мерной плотности распределения могут быть выделены некоторые сечения, соответствующие значениям противоположного аргумента и зависящие от него.
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.