Предмет и задачи курса "Теория вероятности и математическая статистика". Случайные события. Законы распределения непрерывных случайных величин. Математическая статистика, страница 11

Пусть также существует событие А, которое может реализоваться с какой-либо из гипотез. Пусть также известно до опыта вероятности наступления событий-гипотез р(Н₁), р(Н₂),…,р(Н_n). Пусть в этом случае происходит событие А с одной из несовместных гипотез.

А=А*U=А(Н₁+ Н₂+…+ Н_n),

переходя к вероятности события, получим

р(А)=р(А Н₁)+р(А Н₂)+…+р(А Н_n)

Эта формула соответствует теореме сложения, т.е., что произойдет либо А Н₁, А Н₂. Наряду с этим можно применить теорему умножения со следующим определением: Вероятность события А, которое может произойти лишь при условии появления первого из нескольких несовместных событий-гипотез (Н_i)=сумма вероятностей каждой из этих гипотез умноженная на соответствующую условную вероятность появления события А.

р(А)=р(Н₁)*р(А/Н₁)+р(Н₂)*р(А/Н₂)+…+ р(Н_n)*р(А/Н_n) – формула полной вероятности.

Пример: пусть на экзамен первыми вошли 6 студентов среди них 2 отличника (могут сдать экзамен с вероятностью 0,9), 3 хорошиста (могут сдать экзамен с вероятностью 0,8), 1 троечник (могут сдать экзамен с вероятностью 0,3). Какова вероятность сдачи экзамена первым случайно выбранным студентом?

Решение:

Дано р(А/Н₁)=0,9 р(А/Н₂)=0,8 р(А/Н₃)=0,3 условные вероятности наступления события А с одной из гипотез, таким образом, событие АН₁, Н₂, Н₃

Применим формулу полной вероятности.

р(Н₁)=2/6

р(Н₂)=1/2

р(Н₃)=1/6

Определим искомую вероятность сдачи экзамена

р(А)=(1/3)*0,9+(1/2)*0,8+(1/6)*0,3=0,75

Формула полной вероятности позволяет определить наступление события, если априори известны вероятности наступления событий-гипотез, составляющих полную группу (сценарий).

2.13.Формула Байеса

На практике во многих случаях задача переформулируется таким образом, что требуется найти условную вероятность р(Н_i/А). Иначе, если событие А состоялось, то возникает желание определить вероятность реализации событий-гипотез, после того как одна из них уже состоялась. Это позволяет после опыта (апостериори).

р(Н_i/А)= [р(Н_i)*р(А/Н_i)]/р(А),

где р(А) – вероятность события А, вычисляемая по формуле полной вероятности;

i – 1, 2, 3,…,n – текущий индекс событий-гипотез.

Пример: уточним вероятности наступления событий-гипотез в предыдущей задаче апостериори (после того, как сдан экзамен).

р(Н₁/А)=[1/3*0,9]/0,75=0,4

р(Н₂/А)=[1/2*0,8]/0,75=0,53

р(Н₃/А)=[1/6*0,3]/0,75=0,07

Таким образом, формула Байеса позволяет уточнить условную вероятность наступления гипотез после опыта, в результате которого произошло событие.

2.14.Формула Бернулли

В ряде случаев при многократном проведении опыта требуется вычислить вероятность того, что событие произойдет m раз в n испытаниях. Пусть событие А_i если оно состоится будем называть успехом, а если не состоится – неудачей. Тогда вероятность успешных событий будет р(А), а неуспешных событий q(А)=р().

При этом предполагаем, что испытания независимы в совокупности и вероятность появления каждого события одинакова в этом случае:

р(А)=С*р^m*q^n-m,

где С - число сочетаний,

р^m – вероятность наступления успехов,

q^n-m -  вероятность наступления неудач.

Формула Бернулли широко применяется при повторении многократных испытаниях.

С=

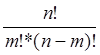
Тогда приходится вычислять не точное число успехов m, а вероятность того, что р=(amb).

В этом случае используется интегральная теорема Муавра-Лапласа

р(amb)=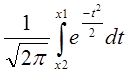

Подынтегральная функция называется функция Лапласа и относится к неберущимся интегралам. Эта функция табулирована и требует определенных навыков для ее определения.

Глава 3.Случайные величины

3.1.Дискретные и непрерывные случайные величины

Случайные величины (СВ) – такие величины, которые в результате некоторого опыта (испытания) принимают то или иное значение, но какое именно – заранее не известно. Является важным элементом любого случайного явления, процесса или технического функционирования. СВ в ряде случаев по своему физическому смыслу характеризуют также случайные события. Обозначают, как и случайные события: A, B, C,…,Y, Z.

Наряду с этим конкретные значения случайной величины обозначаются: х₁, х₂,…,х_n (Х=х_i).

Рассмотрим несколько примеров СВ: