Экономическая оценка инвестиций: Учебное пособие (Конспект лекций и практикум), страница 7

В конце 2011 года произведен депозитный вклад в размере 4 тысяч. Определить какая сумма будет на депозите в конце 2020 года при ежегодном начислении процентов по ставке 8% годовых сложных. Правомочно ли обещание банка о том, что Ваша сумма удвоится?

Период вклада: 9 лет

FV=4´(1+0.08)⁹=8 (обещание правомочно)

Задача 6

Фирма хочет вложить свободные денежные средства в размере 60 000 на три года. Имеется два варианта вложений: а) предоставление кредита с ежегодным начислением 8% сложных; б) предоставление ссуды по ставке 9% (простых). Какой вариант выгоднее для фирмы?

Первый вариант: FV=60000(1+0.08)³=75582.72

Второй вариант: FV=60000(1+3*0.09)=76200

Выгоднее 2-й вариант, т.к. получаемая сумма будет больше.

Задача 7

На какой срок необходимо поместить 1000 долл. под ставку 17% годовых сложных, чтобы получить 3000 долл.?

1000´(1+0,17)^t = 3000

1.17^t = 3;  t = log_1.173 = 7 лет

В реальной жизни проценты могут начисляться с частотой, отличной от 1 раза в год. Наиболее распространены схемы полугодового, ежеквартального, ежемесячного начисления. Если m – количество начислений в году, необходимо преобразовать выведенные нами формулы простого и сложного процента, а именно уменьшить в m раз процентную ставку и увеличить в m раз число периодов.

Схема простого процента никак не реагирует на внутригодовые капитализации:

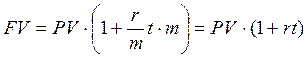
С применением схемы сложного процента результат начнет меняться в зависимости от частоты начисления:

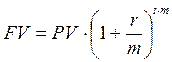                                                               (1.7)

Убедиться в этом можно на примере следующей задачи.

Задача 8

Рассчитайте суммы, накопленные за 1 год на первоначальное вложение в размере 1000 долл. при следующих схемах начисления 12% годовых сложных: а) ежегодное; б) полугодовое; в) ежеквартальное; г) ежемесячное; д) ежедневное начисление. Проанализируйте зависимость накопленной суммы от числа внутригодовых капитализаций.

Из таблицы видно, что с увеличением m накопленная сумма растет. Объясняется это эффектом «процента на процент», т.к. в случае применения схемы сложного процента капитализация происходит на накопленную сумму.

При более глубоком анализе полученных данных можно заметить, что темп прироста накопленной суммы снижается, т.е. каждое последующее увеличение m дает результат меньший, нежели предшествующее. Существует предел, превысить который множитель наращивания не может – это сила роста. Математически ее можно определить по формуле, представленной далее:

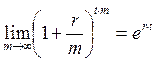                                                                                                     (1.8)

Если m=¥, начисление процентов происходит не дискретно (через заданный временной интервал), а непрерывно. Ступенчатый процесс капитализации преобразуется в сглаженную функцию, а сама схема часто называется схемой непрерывного начисления процентов[1].

В рассмотренной нами задаче PV=1000; r=12%; t=1.

 – значение накопленной суммы в случае применения схемы непрерывного начисления процентов, абсолютный максимум, который может быть получен от внутригодового начисления.

Для возможности корректного сопоставления проектов с различными периодами внутригодового начисления используется показатель т.н. эффективной ставки, которая представляет собой годовую ставку, начисляемую один раз в год и приводящую к тому же результату, что и номинальная при начислении более 1 раза в год.

Рассчитать эффективную ставку можно, воспользовавшись формулой 1.8.

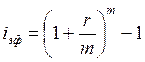, где                                                                                                (1.9)

r – номинальная ставка;

m – количество внутригодовых капитализаций.

Т.е. для варианта ежегодного начисления номинальная и эффективная ставки совпадут (m=1). А дальше они начнут разниться. Понять сущность эффективной ставки можно на примере следующей задачи, основанной на уже произведенных ранее вычислениях.