Экономическая оценка инвестиций: Учебное пособие (Конспект лекций и практикум), страница 14

Графически процесс наращения по сложной процентной ставке иллюстрируется диаграммой на рис. 7.

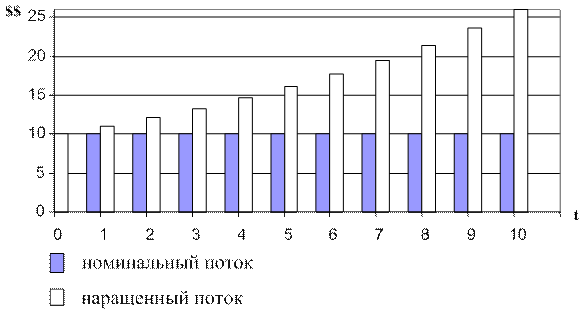
Рис. 7 Наращение по сложной процентной ставке

Задача 50

Рассчитайте будущую стоимость 1000 долларов для следующих ситуаций:

а) 5 лет, 8% годовых, ежегодное начисление процентов;

б) 5 лет, 8% годовых, полугодовое начисление процентов;

в) 5 лет, 8% годовых, ежеквартальное начисление процентов;

г) 5 лет, 8% годовых, ежемесячное начисление процентов.

а)                     в)

б)               г)

2.2.2.  Процесс дисконтирования. Функция настоящей стоимости единицы

Процесс дисконтирования обратен процессу наращения. Примером дисконтирования по схеме простых процентов является уже известный нам учет векселей. В общем случае, математика дисконтирования по простой процентной ставке приведена в табл. 2.2.

Табл. 2.2

Вывод формулы дисконтирующего множителя для схемы простых процентов

Т – время до момента поступления суммы FV.

 – дисконтирующий множитель в условиях действия схемы простых процентов.

В случае действия схемы сложных процентов, по аналогии с процессом наращения, нам придется не умножать, а делить FV на (1+r).

Табл. 2.3

Вывод формулы дисконтирующего множителя для схемы сложных процентов

 – дисконтирующий множитель для схемы сложных процентов или коэффициент дисконтирования. Множитель показывает, во сколько раз уменьшится ценность суммы FV за t периодов при ставке r. Это вторая стандартная функция сложного процента, также называемая настоящая стоимость единицы. Если сумма, ожидаемая к поступлению через t периодов при ставке r, равна 1, дисконтированная, приведенная ее ценность составит . Во втором приложении к пособию приводятся табулированные значения этой стандартной функции сложного процента.

Графически процесс дисконтирования по сложной процентной ставке иллюстрируется диаграммой на рис. 8.

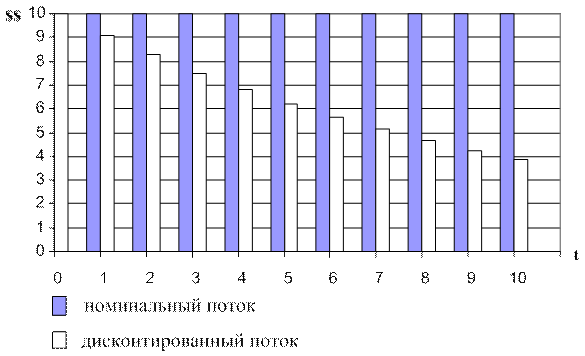
Рис. 8 Дисконтирование по сложной процентной ставке

Задача 51

У Вас есть возможность выбора между получением 5000 долл. через год или 12000 долл. через 6 лет. Каков Ваш выбор, если ставка доходности составляет: а) 12%; б) 20%?

При ставке 12%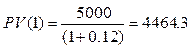                 

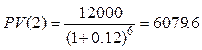
Следует выбрать второй вариант.

При ставке 20%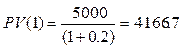                 

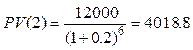
Следует выбрать первый вариант.

2.3.  Оценка потоков с неравными поступлениями. Потоки постнумерандо и пренумерандо

Рассмотренный математический аппарат позволяет приводить к выбранному моменту в настоящем или будущем одну отдельно взятую сумму. Денежный поток – это совокупность доходов и расходов, разрозненных на временной оси. Поэтому для оценки потока в целом необходимо каждую из входящих в него сумм продисконтировать (если приведение осуществляется к настоящему) либо нарастить, если критерием оценки потока служит его будущая ценность.

Очевидно, что для целей такой оценки принципиальное значение имеет одно обстоятельство: в какой момент поступают платежи: в начале или в конце временного интервала? Если платежи поступают в начале периода, поток называется пренумерандо. Если платежи осуществляются в конце, поток называется постнумерандо. Схематично их различие представлено на рис. 9.

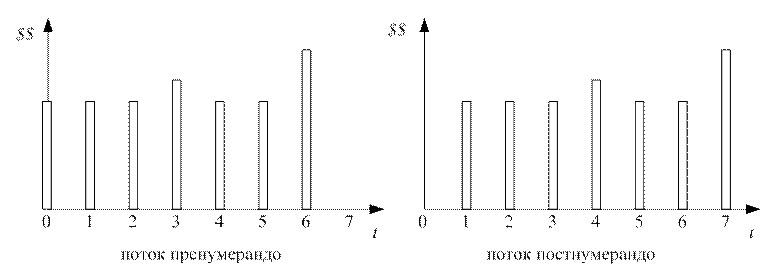
Рис. 9 Различия потоков постнумерандо и пренумерандо

Поток пренумерандо, приведенный к моменту «0», даст тот же результат, что поток постнумерандо, приведенный к точке «1». Следовательно, настоящая ценность потока постнумерандо в текущий момент (0) будет меньше, нежели оценка такого же потока пренумерандо. Различаться оценки будут на величину дисконтирующего множителя .