Пример, приведенный в табл. 5.2, иллюстрирует ситуацию, когда по критерию IRR предпочтительнее проект А. Между тем, если предприятие имеет возможность профинансировать проект В, то безусловно следует предпочесть именно его, поскольку вклад его в увеличение капитала предприятия (NPV) на порядок больше.
2. IRR не позволяет принимать решения в ситуациях, когда цена инвестиционных ресурсов не известна либо меняется (рис. 19). «Улавливать» такие изменения может только критерий NPV.
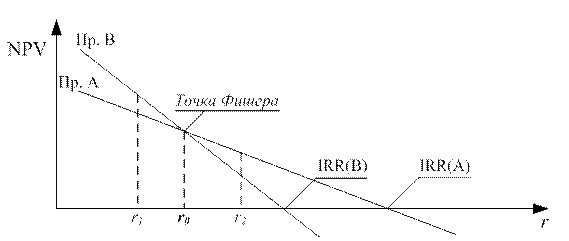
Рис. 19 Точка Фишера
По графикам видно, что по критерию IRR проект А лучше проекта В т.к. IRR (A) > IRR (B). На самом деле если процентная ставка попадает в интервал [0 ; r0], лучше проект В, т.к. в этом случае его NPV больше. Проект А предпочтительнее только в том случае, если реальная ставка будет больше r0.
Точка пересечения графиков на рис. 19 называется точкой Фишера. Ей соответствует уровень пограничной процентной ставки, при которой проекты имеют одинаковый NPV. Для принятия обоснованного решения необходимо сравнить процентную ставку, принимаемую к реализации, с пограничной.
3. IRR не обладает свойством аддитивности.
IRR (A + B) ¹ IRR (A) + IRR (B)
При оценке комбинации проектов, внедряемых одновременно, доходность операции надо рассчитывать путем построения общего денежного потока.
4. Этот критерий абсолютно не пригоден для анализа так называемых неординарных проектов, когда притоки и оттоки капитала чередуются.
Мы уже приводили формулу зависимости NPV = f (r) (5.15). Напомним, что она представляет собой сложное уравнение Т-й степени (Т – продолжительность проекта). IRR – корень этого уравнения. И, в соответствии с правилом Декарта, это уравнение может иметь корней столько, сколько раз меняется знак денежного потока. Иными словами может возникнуть ситуация, когда зависимость NPV (r) из убывающей превратится в одну из следующих (см. рис. 20):
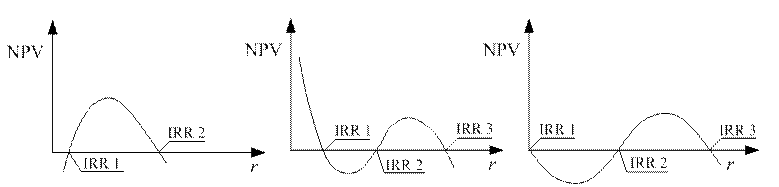
Рис. 20 Возможные виды зависимости NPV =f(r) для неординарных потоков
Т.е. у одного проекта будет несколько значений IRR, и судить о его доходности по этому критерию станет невозможно. В литературе по финансовому анализу можно найти численные примеры таких потоков.
Названные недостатки во многом обусловлены относительностью рассмотренного показателя. Поэтому в практике IRR рассчитывается как бы в дополнение к NPV. Более весомым в процессе принятия решений является критерий чистой приведенной ценности.
NPV и IRR наиболее известны в теории инвестиционного анализа. При этом, опрос британских компаний, проведенный несколько лет назад, показал, что в своей практической деятельности их рассчитывают не более 30% фирм. 90% указали, что пользуются при оценке проектов критерием срока окупаемости. Схожая ситуация существует и в других странах, в т.ч. и в России. Всем известно понятие срока окупаемости, смыл этого показателя достаточно легко интерпретировать, и в отличие от рассмотренных выше критериев его достаточно легко рассчитать, что и обеспечило сроку окупаемости такую распространенность. Здесь отметим, что к расчету срока окупаемости существует несколько подходов, и не все они математически просты.
Простейшая трактовка срока окупаемости на языке уже известных нам денежных потоков выглядит следующим образом:
Срок окупаемости (Payback Period – PP) – это минимальный период времени в течение которого капитальные вложения будут погашены доходами от них.
![]()
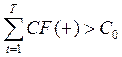 (5.16)
(5.16)
Согласно данного подхода срок окупаемости рассчитывается методом суммирования положительных потоков (доходов, поступлений, эффектов) до того момента, пока полученный результат не превысит величины первоначальной инвестиции. Простота – единственное достоинство данного метода. Недостатков же довольно много.
1. PP не учитывает влияние доходов последних периодов (см. табл. 5.3).
Табл. 5.3
Данные по проектам для выявления первого недостатка PP
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.