Экономическая оценка инвестиций: Учебное пособие (Конспект лекций и практикум), страница 18

 - настоящая стоимость единичного аннуитета, четвертая функция сложного процента. Функция показывает, какова настоящая ценность потока, состоящего из t равномерных платежей размером в единицу каждый при начислении ставки r через период их поступления. Некоторые значения этой функции приводятся в приложении 4. Стандартные значения соответствуют потоку постнумерандо.

Задача 64

Определите текущую рыночную стоимость ценной бумаги, обеспечивающей своему обладателю ежегодный доход в размере 500 у.е. на протяжении 5 лет (действующая годовая ставка 15%).

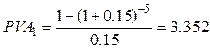
Цена бумаги: 500*3,352=1676 у.е.

Задача 65

Определите текущую стоимость купонной облигации номиналом 5000 со сроком погашения через 4 года. Ставка купонного дохода 8% годовых. Доходы можно безрисково инвестировать под 9% годовых с ежеквартальным начислением.

Купонная облигация - облигация, по которой владельцу выплачивается не только номинальная стоимость в момент погашения, но и периодический купонный процент. Считается, что купонная облигация содержит отрезные купоны, по которым после определенного срока выплачивается процентный доход.

Доход от облигации складывается из аннуитета постнумерандо (настоящую стоимость которого и нужно определить), а также последней выплаты размером в номинал, которая также должна быть приведена к текущему моменту.

Настоящая стоимость аннуитета (размер платежа 5000*0,08=400):

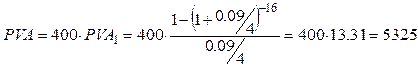
Приведенная стоимость последнего платежа:

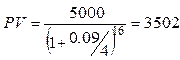
Текущая стоимость такой облигации составляет 5325+3502=8827

Схема для расчета настоящей стоимости аннуитета пренумерандо приведена на рис. 15.

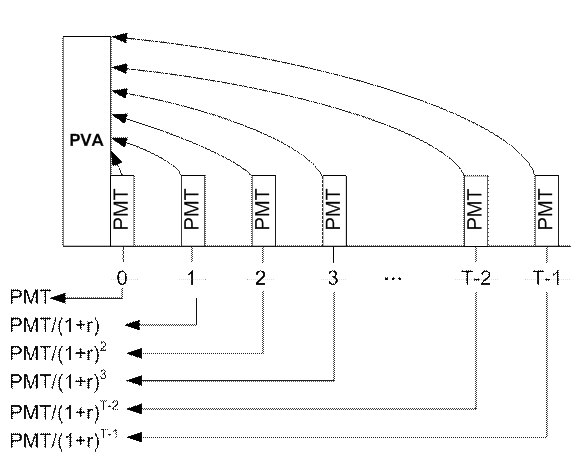
Рис. 15 Расчет настоящей стоимости аннуитета пренумерандо

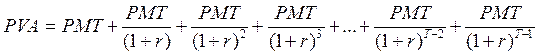
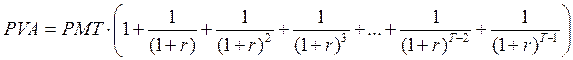                  (3.9)

Параметры прогрессии в этом случае следующие:

; ;

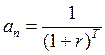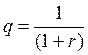
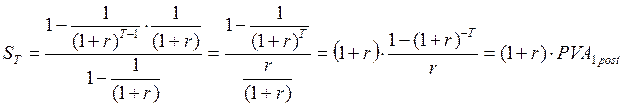
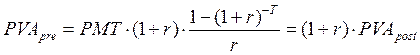                                              (3.10)

Аннуитет пренумерандо всегда «дороже» на один множитель наращения, равно как и в случае с неравномерными потоками.

Для бессрочного аннуитета определение будущей стоимости не имеет смысла. Единственной его оценкой служит настоящая стоимость. Поскольку поток бесконечен, для расчета нужно использовать формулу бесконечно убывающей геометрической прогрессии:

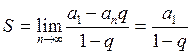                                                                                            (3.11)

Настоящая ценность бесконечного потока платежей (в соответствии с формулой 3.11) составит:

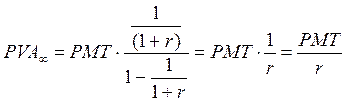                                                             (3.12)

В разделе 1.2 мы упоминали формулу Карла Маркса для расчета цены земли. Рента за пользование землей представляет собой пример бессрочного аннуитета.

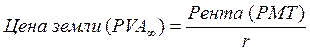                                                                    (3.13)

В англоязычной литературе бесконечные аннуитеты называются особым термином – perpetuity.

Задача 66

Клиент предложил оплатить выполненную работу одним из двух способов: а) единовременно получить 5000 долл. или б) два года спустя получать бесконечно долго по 500 долл. ежегодно в начале каждого года. Какой вариант более предпочтителен, если приемлемая норма прибыли 8%?

Необходимо рассчитать настоящую стоимость бесконечного аннуитета с платежом 500, а затем привести ее к текущему моменту (продисконтировать на два года).

На настоящий момент это:

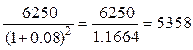
Следовательно, второй вариант (б) выгоднее.

3.4.  Взнос на амортизацию единицы и коэффициент фонда возмещения

При оценке аннуитетов правомочна постановка обратной задачи: определить величину разового взноса при известной настоящей либо будущей стоимости. Исходя из материалов разделов 3.2 и 3.3,

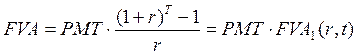 (формула 3.3)

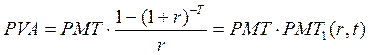 (формула 3.7)

Следовательно, величины взносов (PMT) определяются по формулам:

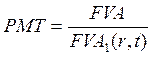 для потока с известной будущей (накопленной) стоимостью;

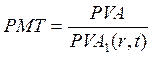 для потока с известной настоящей (приведенной) стоимостью.

Величины, обратные FVA₁ и PVA₁, представляют собой пятую и шестую стандартные функции сложного процента и имеют собственные названия и экономическую интерпретацию:

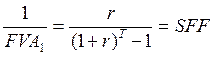                                                                                       (3.14)