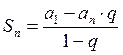 , где (3.2)
, где (3.2)
![]() - первый член ряда;
- первый член ряда;
![]() - последний член ряда;
- последний член ряда;
q – знаменатель геометрической прогрессии. ![]()
![]() =1;
=1; ![]() ;
; ![]()
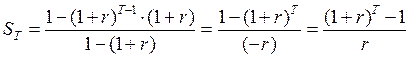
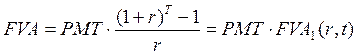 (3.3)
(3.3)
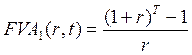 (3.4)
(3.4)
![]() - будущая
стоимость единичного аннуитета, третья стандартная табулированная
функция сложного процента, позволяющая для любых значений r и t
определить ценность наращенного потока, умножив величину взноса (PMT) на
значение функции. Физический смысл FVA1 заключается в следующем:
функция показывает, чему равна будущая стоимость потока из t единичных
платежей при ставке r. В англоязычной литературе эту функцию называют
CVFA (Compound Value Factor for an Annuity).
С применением компьютера ее достаточно легко рассчитать. Как альтернатива,
можно воспользоваться финансовыми таблицами. Третье приложение к настоящему
пособию содержит таблицу значений FVA1 для некоторых значений
периодов и процентных ставок.
- будущая
стоимость единичного аннуитета, третья стандартная табулированная
функция сложного процента, позволяющая для любых значений r и t
определить ценность наращенного потока, умножив величину взноса (PMT) на
значение функции. Физический смысл FVA1 заключается в следующем:
функция показывает, чему равна будущая стоимость потока из t единичных
платежей при ставке r. В англоязычной литературе эту функцию называют
CVFA (Compound Value Factor for an Annuity).
С применением компьютера ее достаточно легко рассчитать. Как альтернатива,
можно воспользоваться финансовыми таблицами. Третье приложение к настоящему
пособию содержит таблицу значений FVA1 для некоторых значений
периодов и процентных ставок.
Отметим, что значения стандартных функций выведены для потока постнумерандо.
Задача 60
Ваш ежемесячный вклад составляет 200. Достаточно ли этого, чтобы через два года собрать 5000 (8% годовых сложных, ежемесячное начисление, взносы в конце каждого месяца)?
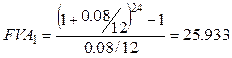 ; FVA
= 25.933*200 = 5186.6 (достаточно)
; FVA
= 25.933*200 = 5186.6 (достаточно)
Задача 61
Ваш ежемесячный вклад составляет 300 ед. Хватит ли этой суммы для того, чтобы к концу второго года собрать 8300? (11% годовых сложных, ежемесячное начисление, взносы в конце каждого месяца)
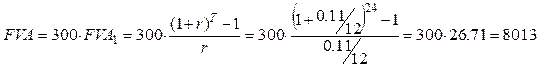 (не достаточно)
(не достаточно)
Приведение потоков пренумерандо осуществляется аналогично. Процесс наращения в этом случае несколько отличается и соответствует схеме на рис. 13.
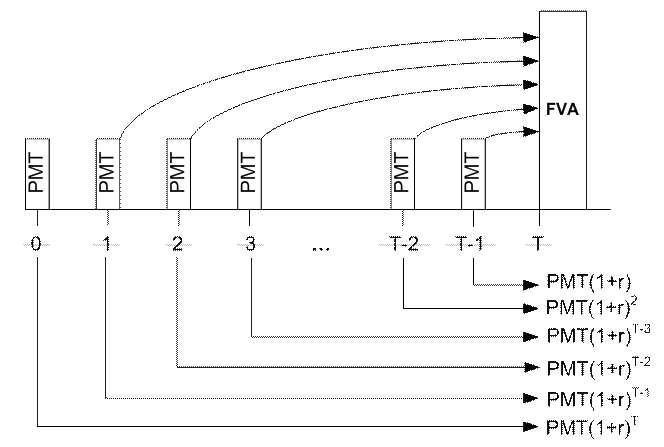
Рис. 13 Расчет будущей стоимости аннуитета пренумерандо
![]()
![]()
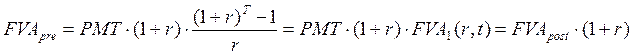 (3.5)
(3.5)
Задача 62
Если в задаче №60 взносы будут осуществляться в начале каждого месяца, то сможет ли вкладчик собрать к концу года сумму в 5500?
![]()
Задача 63
Солидная страховая компания предлагает желающим заключить договор, согласно которому можно накопить значительную сумму своему ребенку. Суть договора в следующем. В первые 3 года после рождения ребенка вы платите компании по 1000 долл. ежегодно, в следующие 2 – по 1500 долл. (схема постнумерандо). В дальнейшем деньги лежат на специальном счете до совершеннолетия вашего ребенка (18 лет), когда вы можете получить 18000 долл. Стоит ли участвовать в этом необычном инвестиционном проекте, если приемлемая норма прибыли равна 8%? Решите эту же задачу, если по истечении 5 лет с момента заключения договора процентная ставка будет понижена до 6%.
Момент приведения – конец пятого года. К этой точке сводятся два аннуитета, а далее полученная сумма наращивается в течение 13 лет (по ставке 8% и по ставке 6%). Результат расчетов сравниваем с 18000.
Приводим первый аннуитет. 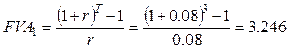
![]() (значение на конец третьего года дополнительно
приводится к концу 5-го мультиплицирующим множителем
(значение на конец третьего года дополнительно
приводится к концу 5-го мультиплицирующим множителем ![]() ,
т.к. эти деньги пролежат на счету еще 2 года).
,
т.к. эти деньги пролежат на счету еще 2 года).
Приводим второй аннуитет. 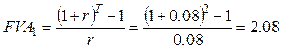
![]()
При ставке 8% к совершеннолетию малыша получится:
![]() (участвовать не стоит, т.к. альтернативы
дадут больше)
(участвовать не стоит, т.к. альтернативы
дадут больше)
При ставке 6% к совершеннолетию получится:
![]() (участвовать стоит, в банках накопится
меньшая сумма)
(участвовать стоит, в банках накопится
меньшая сумма)
Настоящая стоимость аннуитетного потока (Present Value of an Annuity) традиционно обозначается аббревиатурой PVA.
Для потока постнумерандо логика приведения показана на рис. 14. В соответствии с рисунком,
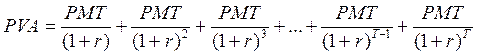
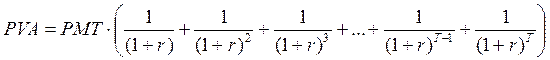 (3.6)
(3.6)
Параметры прогрессии в этом случае следующие:
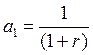 ;
; 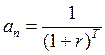 ;
; 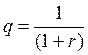
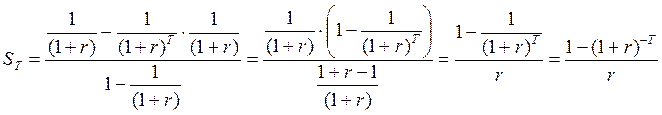
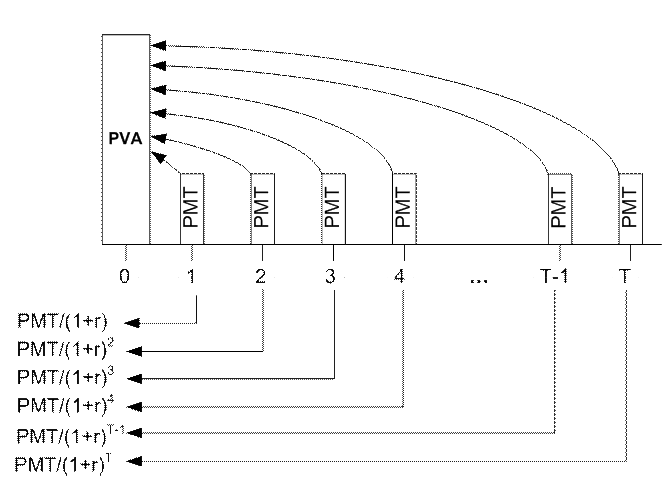
Рис. 14 Расчет настоящей стоимости аннуитета постнумерандо
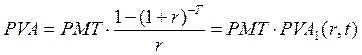 (3.7)
(3.7)
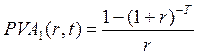 (3.8)
(3.8)
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.