SFF – коэффициент фонда возмещения (Sinking Fund Factor) – величина разового платежа, аннуитетный ряд из которых продолжительностью T даст при ставке r будущую стоимость потока, равную единице.
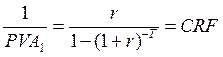(3.15)
CRF – взнос на амортизацию единицы или коэффициент покрытия (Capital Recovery Factor или Capital Recovery and Loan Amortisation) – величина разовой выплаты, аннуитетный ряд из которых за T периодов при ставке r полностью покроют фонд размером в единицу.
Задача 67
Чему должен быть равен ежемесячный вклад по условиям задачи №61, чтобы накопленной суммы хватило?
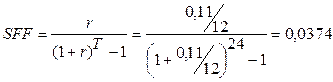
Задача 68
Вам предлагают ежегодно на протяжении 10 лет делать взнос в размере 3000 долл. с целью потом, также на протяжении 10 лет, получать из накопленного фонда содержание (на оба варианта выплат действует схема постнумерандо). Определите размер ежегодного содержания, если по взносам начисляется 15% годовых с ежегодным начислением.
Определяем величину фонда:
долл.
Задача 69
Вам необходимо накопить 25 тыс. долл. за 8 лет. Каким должен быть ежегодный взнос в банк (схема пренумерандо), если банк предлагает 10% годовых? Какую сумму нужно было бы единовременно положить в банк сегодня, чтобы достичь той же цели?
Нужно рассчитать функцию коэффициента фонда возмещения, а затем не забыть что аннуитет пренумерандо.
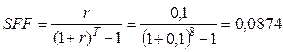- стандартная функция
коэффициента фонда возмещения.
Будущая стоимость потока пренумерандо 25 тыс. Для потока постнумерандо:
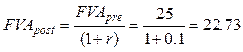
Величина взноса 22,73*0,0874=1,9874 тыс. долл.=1987,4 долл.
Ищем размер единовременного вклада:
тыс.
долл.
Несовпадение частоты взносов (выплат) и начислений процентов – довольно частое явление при реализации различных накопительных и амортизирующих схем. При этом, игнорирование структурной сущности потока в такой ситуации может привести к результатам расчетов, противоречащим природе финансовых вычислений, в чем нам предстоит убедиться на конкретных примерах. На грубые ошибки всегда укажет и решение задачи «прямым счетом». Поэтому в каждой конкретной ситуации следует сначала убедиться, что периоды взносов и начислений совпадают, а затем применять к ним рассмотренные ранее методы решения и стандартные финансовые функции.
Если частоты не совпадают, можно столкнуться с двумя ситуациями:
1. Частота взносов меньше частоты начисления процентов (взносы либо выплаты осуществляются реже периода капитализации);
2. Поступления (выплаты) осуществляются чаще, чем финансовое учреждение начисляет проценты на них.
Методики расчетов для этих двух ситуаций различны, поэтому их целесообразно рассмотреть подробнее
В данной ситуации начисление процентов на величину каждого взноса осуществляется несколько раз. Поэтому к концу каждого периода взноса на счете образуется сумма, равная
, где
m – количество начислений в рамках периода взносов (выплат);
r – номинальная процентная ставка, соответствующая периоду начисления (месячная, квартальная и т.п.).
Оценка такого аннуитета сводится к вычислению
финансово эквивалентной ставки 
, соответствующей
периоду осуществления взносов. Не сложно заметить, что если период аннуитета
равен 1 году, это эффективная процентная ставка. В этом отношении, эффективные
ставки являются разновидностью эквивалентных.
Далее аннуитет можно оценивать по стандартным рассмотренным ранее методикам, применив в расчетах пересчитанное значение процентной ставки.
Аннуитеты пренумерандо можно преобразовывать к потокам постнумерандо путем расчета суммы, образующейся на счете к концу каждого периода и далее заменять в формулах и ставку на эквивалентную, и величину взноса на полученную в ходе приведения к концу периода.
Задача 70*
Вы имеете возможность в течение 5 лет вносить в банк каждые полгода по 1000 долл. по схеме пренумерандо. Банк начисляет 12% годовых: а) раз в полгода; б) ежеквартально; в) ежемесячно. Какая сумма будет на счете в конце срока?
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.