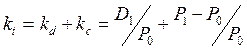Экономическая оценка инвестиций: Учебное пособие (Конспект лекций и практикум), страница 31

                                                                                   (5.6)

P₀ – текущая рыночная стоимость финансового актива (величина первоначальной инвестиции, цена приобретения);

P₁ – ценность актива через один временной интервал;

D₁ – ожидаемый к получению через время t доход$

k_d – дивидендная (купонная, текущая) доходность инвестиции;

k_c – капитализированная доходность;

k_t – общая доходность актива.

Отметим, что соотношение k_d и k_c в каждом случае различно (из формулы 5.6 хорошо видно, что k_c может быть отрицательной величиной). Таким образом, инвестор всегда должен расставлять приоритеты – что важнее: получение дивидендного дохода или прирост капитализации.

Формулу 5.6 можно легко вывести и из уравнения денежного потока. Для простейшего варианта инвестиции, когда вложение инвестора однократное, эффективность оценивается, как

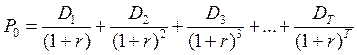                                                             (5.7)

P₁ представляет собой такую же дисконтированную оценку, но с позиции момента t:

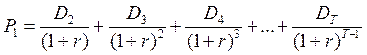                                                           (5.8)

Тогда выражение 5.7 можно переписать следующим образом:

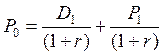                                                                                                    (5.9)

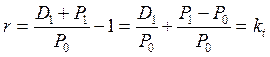                                                                            (5.10)

Наиболее показательным примером применения этих формул служит оценка срочных купонных облигаций. Поток доходов от такой облигации складывается из аннуитета постнумерандо продолжительностью n – время до погашения, а также последней выплаты номинала облигации или ее нарицательной стоимости. Текущая цена приобретения определяется рынком и, как правило, известна на момент оценки целесообразности инвестирования.

                                                                                 (5.11)

F – номинал облигации (ее нарицательная стоимость).

Разрешив уравнение относительно r, получим общую доходность приобретения такой облигации (доходность к погашению, YTM – Yield to Maturity). На практике часто используют упрощенную формулу, дающую при этом, достаточно точный результат:

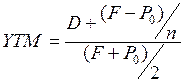                                                                                             (5.12)

Если в данной формуле номинал заменить выкупной ценой в момент отзыва облигации, а вместо n подставить время до отзыва (досрочного погашения), получим показатель доходности досрочного погашения (YTC – Yield to Call), применяемый для оценки отзывных облигаций (облигаций с правом досрочного погашения).

Задача 136

Рассчитать общую доходность облигации нарицательной стоимостью 100 тыс. руб. с годовой купонной ставкой 9%, имеющей текущую рыночную цену 84 тыс. руб. Облигация будет приниматься к погашению через 8 лет. Чему равна доходность досрочного погашения такой облигации, если отзыв может состояться через 5 лет, а выкупная цена превышает номинал на величину годовых процентов?

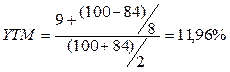
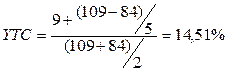
Решение по формуле 5.11 дает абсолютно точные результаты на уровне YTM=12,25% и YTC=15.11%, что позволяет считать точность формулы 5.12 приемлемой.

В общем случае, инвестиция совсем не обязательно осуществляется единовременно. Конфигурация денежного потока может быть любой. Тогда P₀ в формуле 5.7 должно быть заменено на приведенную ценность всех осуществляемых инвестором вложений.

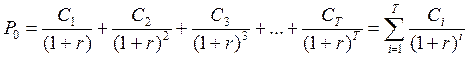                                    (5.13)

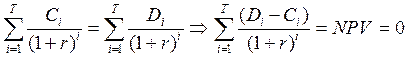                                                    5.14

Выведенное нами выражение 5.14 представляет собой условие для определения доходности любой инвестиции. Чтобы вычислить эту доходность, достаточно разрешить уравнение относительно r. Эта доходность имеет в финансовом анализе свое название и четкую экономическую интерпретацию, поскольку наравне с NPV является одним из основных критериев оценки инвестиционных проектов.

Internal Rate of Return (IRR) также имеет несколько вариантов перевода:

-  внутренняя норма отдачи или норма рентабельности инвестиций;

-  ставка внутренней доходности;

-  ставка внутренней ренты или просто внутренняя рента проекта и т.д.