Экономическая оценка инвестиций: Учебное пособие (Конспект лекций и практикум), страница 20

а) аннуитет пренумерандо с совпадающей частотой взносов и начислений процента.

б) взносы реже начислений, m = 2, r = 3%.

 или

в) взносы реже начислений, m = 6, r  = 1%.

Задача 71*

На протяжении 3-х лет Вы получали от родителей по 4000 в год (в начале). Какая сумма накопится на вашем счете к концу третьего года? Сколько нужно было бы вносить ежемесячно, чтобы сумма, накопленная за те же три года, была равна 20000 (15% годовых сложных, ежемесячное начисление).

Первый вариант – аннуитет пренумерандо. Поскольку начисление процентов ежемесячное, необходимо преобразовать его к аннуитету постнумерандо, рассчитав будущие стоимости взносов размером по 4 тыс. к концу года при ежемесячном начислении.

PMT'=4000*(1+0.15/12)¹²=4643

Затем ищем эффективную ставку, соответствующую 15% сложных при ежемесячном начислении:

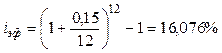
Теперь можно рассчитать будущую стоимость аннуитета с размером взноса 4643, осуществляемым ежегодно при годовой ставке 16,076%. Аннуитет идет 3 года.

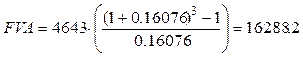
Для определения ежемесячного взноса при известной накопленной сумме в 20000 используем стандартную функцию коэффициента фонда возмещения.

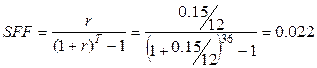
Размер взноса

3.5.2.  Аннуитеты с частотой выплат больше периода начисления процента

В случае, когда взносы либо выплаты осуществляются чаще периода начисления процента, имеет место следующая схема капитализации:

На первый платеж начисляются проценты за весь период. На второй платеж – проценты за часть периода, меньшую на один интервал поступления средств. На третий платеж проценты будут начислены за часть периода, меньшую на два интервала поступлений и т.д. На последний взнос банк начислит проценты только за один период поступления, т.к. деньги находились в распоряжении банка именно на протяжении этого срока. Математически сумма к концу первого года формализуется следующим образом:

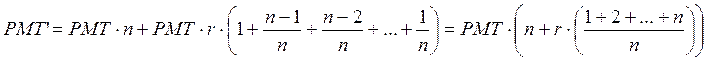
Числитель в скобках – сумма натурального ряда от 1 до n, рассчитываемая по формуле

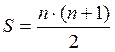                                                                                                           (3.16)

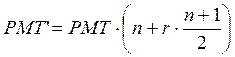                                                                                   (3.17)

Теперь такой поток может рассматриваться как аннуитет постнумерандо с размером взноса, определенным по выведенной выше формуле, номинальной процентной ставкой и совпадающими периодами начисления.

Задача 72*

Вы имеете возможность в течение 5 лет вносить в банк каждые полгода по 1000 долл. по схеме пренумерандо. Банк начисляет 12% годовых ежегодно. Какая сумма будет на счете в конце срока?

Взносы чаще начисления.

Задача 73*

В течение ближайших четырех лет вы планируете вносить в банк по 500 долл. в начале каждого полугодия, затем в течение трех лет – по 750 долл. ежегодно (схема пренумерандо). Банк начисляет проценты ежегодно по ставке 12% годовых. Какая сумма будет на счете к концу финансовой операции (т.е. через 7 лет)?

Для первого потока не совпадают периоды взносов и начислений процента. Но считать этот поток эквивалентным потоку со взносом в 1000 нельзя. Первые 500 пролежат 4 года, вторые 500 пролежат 3,5 года, третьи 3 года и т.д. Последние (восьмые) 500 пролежат полгода (поток пренумерандо). В рамках каждого из 4-х лет к концу года будет накоплена сумма

Т.е. наш поток теперь можно представить как поток постнумерандо с размером выплаты 1090, числом периодов 4 и ежегодной выплатой 12%.

Эти деньги пролежат еще 3 года, и к концу финансовой операции их накопится

У второго потока периоды взносов и начислений совпадают. Сумма, полученная для схемы постнумерандо, должна быть приведена к концу множителем (1+r).

;

Задача 74*

Изменится ли накопленная сумма в условиях задачи №73, если проценты будут начисляться раз в полгода? Если изменится, то в какую сторону? Сначала обоснуйте свой ответ, не делая вычисления, а затем подтвердите его расчетами. Сравните полученный результат с ответом в предыдущей задаче.