Экономическая оценка инвестиций: Учебное пособие (Конспект лекций и практикум), страница 6

Очевидно, что функция простого процента линейная, процентная ставка r выступает в ней коэффициентом линейной функции (определяет угол наклона графика).

Задача 1

Вклад в размере 1000 долл. осуществлен на условиях начисления простой годовой ставки 12%. Рассчитайте суммы, которые будут на счете через 1, 2, 3 года? В какой зависимости находятся полученные значения?

FV₁=1000´(1+1´0.12)=1120

FV₂=1000´(1+2´0.12)=1240

FV₃=1000´(1+3´0.12)=1360

Зависимость линейная.

Задача 2

На какой срок необходимо поместить денежную сумму под простую процентную ставку 8% годовых, чтобы она увеличилась в полтора раза?

PV(1+0,08t)=1.5PV

0.08t=0.5;               t=6.25 лет

Схема простых процентов применяется преимущественно при незначительных сроках финансовых операций, когда начисление процента на капитал предусмотрено единожды. Другим распространенным примером применения схемы простых процентов служат операция учета векселей.

Вексель – ценная бумага, представляющая собой обязательство выплатить его держателю определенную сумму в обозначенный момент времени. Сумма к погашению называется номиналом векселя (F). Номинал может быть задан фиксировано либо с учетом процентов на срок долга. Сумма, по которой такая ценная бумага может быть продана в заданный момент времени, называется учетной стоимостью (P) и определяется по формуле:

, где                                                                                                      (1.6)

n – время до погашения векселя;

d – учетная ставка.

Очевидно, что P всегда меньше F. Разница (F-P)=Fnd представляет собой получаемые банком комиссионные. Очевидно, что стоимость ценной бумаги будет возрастать с приближением срока уплаты по векселю и, напротив, снижаться, если n растет. Из формулы (1.6) вытекает, что n должно быть меньше 1/d, в противном случае величина дисконтного множителя и суммы P будет отрицательной, т.е. при большом сроке n учет векселя теряет экономический смысл.

Задача 3

Вексель учтен банком по учетной  ставке 20% годовых простых по цене 5000 за 3 года до срока уплаты по векселю. Каков номинал векселя?

d=20%; P=5000; n=3

F=P/(1-nd)=5000/(1-3*0.2)=12500

Задача 4

Господин N выписал вексель с обязательством вернуть 10 000 через 4 года. По какой цене этот вексель будет учтен банком через 1, 2, 3 года с учетной ставкой 20% годовых простых?

F=10000

n=3 через год (4-1)             P1=10000(1-3*0.2)=4000

n=2 через 2 года (4-2)        P2=10000(1-2*0.2)=6000

n=1 через 3 года (4-3)        P3=10000(1-1*0.2)=8000

Очевидно, что суммы, получаемые при изменении срока до погашения, также как и в рассмотренных ранее задачах, находятся в линейной зависимости.

1.3.2.  Схема начисления сложного процента. Внутригодовое начисление процентов. Схема непрерывного начисления процентов. Понятие эффективной ставки

Сложный процент (англ. compound interest) – схема начисления, при которой капитализация происходит на накопленную сумму с учетом процентов за прошлые периоды. По аналогии с разделом 1.3.1, выведем расчетную формулу для этого случая (табл. 1.2).

Табл. 1.2

Капитализация при начислении сложного процента

Функция сложного процента степенная, ее вид, а также взаимозависимость со схемой простого процента представлены на рис. 1.3.

Из рисунка видно, что при сроке 1 год (а точнее 1 период начисления) схемы простого и сложного процентов равноценны [FV= PV´(1+r)]. При сроках инвестирования менее периода начисления процента (t < 1) вкладчику выгоднее схема простого процента. При значениях t более 1 периода сложный процент дает большую накопленную сумму, нежели простой.

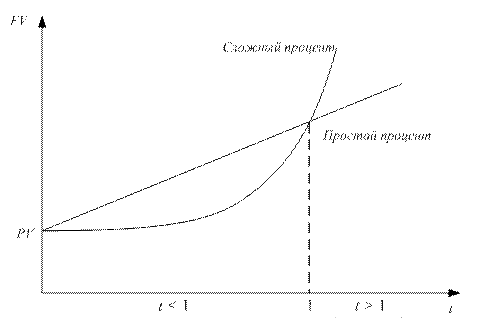
Рис. 1.3 Схемы начисления простого и сложного процента

Задача 5