Экономическая оценка инвестиций: Учебное пособие (Конспект лекций и практикум), страница 5

В результате деньги приобрели характеристику, ранее не ведомую широким кругам – временную ценность. Первый аспект этой временной ценности связан с существованием инфляции, т.е. постепенным падением покупательной способности. Второй аспект обусловлен возможностью пускать деньги в оборот, работать на себя и на своего владельца.

Альтернативы вложения и необходимость управлять деньгами существуют не только у юридических, но и у физических лиц (простых граждан). Поэтому знание экономических основ этой деятельности в любом случае пригодится даже в бытовой жизни. Учет временной ценности влечет одно важное обстоятельство. Не правомочно становится напрямую отождествлять (складывать, сравнивать) денежные суммы, которые образуются в различные периоды времени. Они не одинаковы по свой сути, не равноценны. То, что будет получено завтра, имеет ценность большую, чем то, что будет получено по прошествии нескольких лет. За эти несколько лет деньги могли бы принести доход в обороте, их стало бы больше.

Введение понятия ценности предполагает существование цены, ориентируясь на которую можно приводить денежные потоки «к общему знаменателю». Цена денег – процентная ставка – может быть получена из следующего простейшего примера (рис. 1.1).

Рис. 1.1 Логика осуществления финансовых операций

Представим, что один человек предоставляет другому в долг некоторую сумму при условии, что через время t будет возвращена сумма большая. Сумма, предоставляемая в долг, называется Present Value (PV – настоящая сумма). Возвращаемое количество называется Future Value (FV – будущая сумма).

Результат такой сделки может быть измерен разницей (FV – PV). Но в этом случае будут иметь место серьезные недочеты. Во-первых, не понятно, за какой период времени получен эффект (100 долл. за месяц, год, день или десятилетие). Во-вторых, каким был размер первоначального вложения, вернувшегося с прибавкой (1000 долл. при вложенных 2000, 10000, 1 млн. и т.п.). (FV – PV) – это эффект, результат. Эффективность – категория относительная.

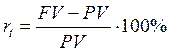 - процентная ставка или цена денег                                    (1.3)

Если t равно 1 году, ставка годовая; если t – 1 квартал, ставка квартальная; t = 1 месяц – ставка месячная и т.д. Совпадение единиц измерения самих денег как ресурса, и их цены дает безразмерную категорию процента.

Ставка r_t называется «процент», «рост», «норма прибыли», «доходность», «темп прироста». По аналогии, может быть рассчитана ставка d_t, именуемая «дисконтом», «темпом снижения» или учетной ставкой.

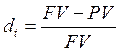                                                                                                            (1.4)

Сфера применения дисконта довольно ограничена. В основном, он применяется в банковском секторе, в частности, для учета векселей.

Между процентом и дисконтом существует взаимозависимость:

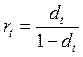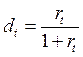;                                                                                                  (1.5)

Ставка роста всегда больше ставки дисконта, причем величина различия определяется уровнем процентных ставок. При r_t=8% d_t,=7,4%. При r_t=80% d_t,=44,4%. Вид взаимозависимости иллюстрируется графиками на рис. 1.2.

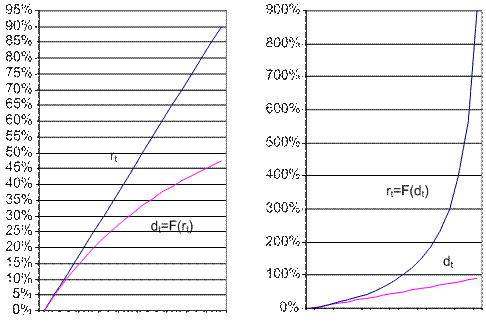
Рис. 1.2 Взаимозависимость простой и учетной ставок

В зависимости от того, что является базой капитализации (начисления процентной ставки), различают несколько схем или методов начисления процентов, которые подробно рассмотрены далее.

1.3.1.  Схема начисления простого процента и области ее применения

Простой процент (англ. simple interest) – это простейшая схема, в соответствии с которой проценты начисляются на фиксированную сумму первоначального вложения.

В этом случае имеет место следующий процесс капитализации:

Табл. 1.1

Капитализация при начислении простого процента