в) 200 тыс. сразу, 300 тыс. через два года
г) вексель на два года номиналом 500 тыс. с процентами по ставке 10% сложных с полугодовым начислением.
Стоимость денег 12% годовых, начисление ежегодное. Учетная ставка по векселям – 8% годовых.
Задача 58
Предприятие имеет возможность участвовать в некоторой деловой операции, которая принесет доход в размере 10 млн. руб. по истечении 2-х лет. Ответьте на следующие вопросы:
1. Если имеются два варианта получения доходов: либо по 5 млн. руб. по истечении каждого года, либо единовременное получение всей суммы в конце двухлетнего периода, то какой из них более предпочтителен?
2. Существуют ли такие условия, когда выбор вариантов для вас безразличен?
3. Изменится ли ваше решение, если доход второго года уменьшится до 4 млн. руб.?
Задача 59
Оплата по долгосрочному контракту предполагает выбор одного из двух вариантов: 25 млн. руб. через 6 лет или 50 млн. руб. через 12 лет. При каком значении процентной ставки выбор безразличен?
Термин «аннуитет» происходит от латинского слова anno – год. Это особая разновидность денежного потока, возникающая в случае выполнения двух условий: все платежи в таком потоке равны по величине и равномерно распределены во времени (осуществляются через равные временные интервалы).
Если названные условия не выполняются, поток называется неравномерным или не регулярным. Аннуитеты часто называются равномерными или регулярными потоками.
В реальной жизни ситуация аннуитета возникает достаточно часто. Это и рентные платежи за пользование землей, и выплаты кредитов равными долями ежегодно или ежемесячно, и получение фиксированных доходов на некоторые разновидности ценных бумаг (привилегированные акции, купонные облигации).
Если аннуитет ограничен по времени (известно точное число выплат), он называется срочным. Если количество интервалов бесконечно или очень велико (40, 50 и более лет), такой аннуитет называется бессрочным (в англоязычной литературе к нему применяется специальный термин – perpetuity). Примерами бессрочных потоков являются долгосрочная аренда земельных участков, пожизненные выплаты содержания или доходов на капитал, бессрочные облигации, рента за пользование съемным жильем без права его выкупа.
В общем случае, можно выделить 4 типа аннуитетных потоков с позиции их экономической оценки (рис. 11):
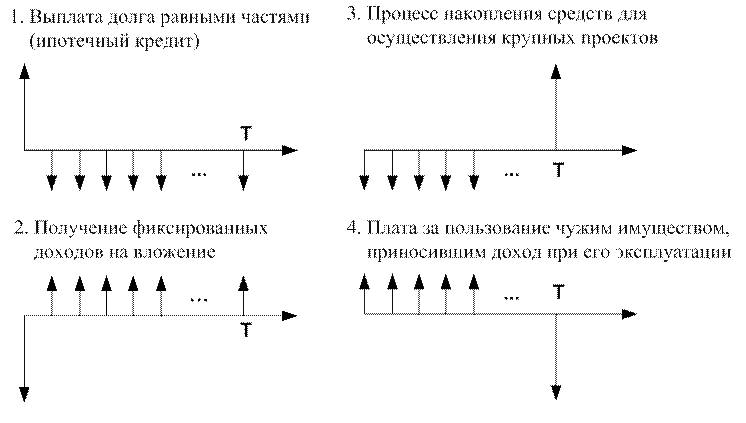
Рис. 11 Практическая интерпретация аннуитетных денежных потоков
Очевидно, что в первых двух ситуациях необходимо получить обобщенную оценку аннуитета на текущий момент (привести поток к настоящему). Сравнение этой оценки с величиной кредита или инвестиции позволит понять, целесообразна ли финансовая операция. В случаях 3 и 4 нужна будущая ценность аннуитета, приведение его к точке T. Такую оценку можно осуществить способами, рассмотренными ранее для нерегулярных cash flow. Но специфика аннуитетов – их равномерность – серьезно упрощает эту задачу.
При оценке аннуитетов традиционно используются следующие аббревиатуры и обозначения:
PMT (англ. payment) – величина платежа, поток которых оценивается;
FVA (Future Value of an Annuity) – будущая стоимость аннуитета[2].
Общая логика задачи приведения схематично представлена на рис. 12 и рис. 13 для потоков постнумерандо и пренумерандо соответственно.
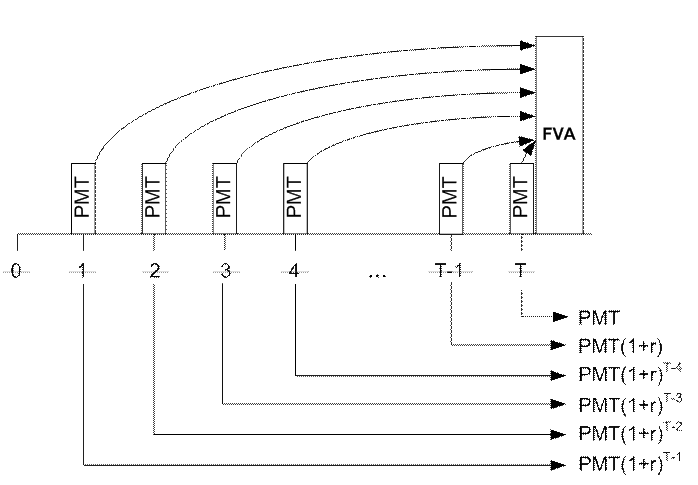
Рис. 12 Расчет будущей стоимости аннуитета постнумерандо
Искомый критерий будущей стоимости равномерного потока представляет собой сумму формирующих его взносов, каждый из которых приведен к моменту T соответствующим ему коэффициентом наращения.
Для потока постнумерандо (рис. 12):
![]()
![]() (3.1)
(3.1)
Особенность аннуитетного потока, позволяющая упростить расчеты по его оценке, собственно, и связана с тем, что ряд в скобках представляет собой геометрическую прогрессию, сумма n членов которой может быть получена по известной формуле:
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.