Экономическая оценка инвестиций: Учебное пособие (Конспект лекций и практикум), страница 35

Рассмотренные критерии окупаемости инвестиций рассчитываются очень легко, но часто не позволяют разрешить задачи, возникающие не в теории, а в реальной жизни. Так, часто инвестор хочет знать срок окупаемости точнее целого числа лет. Вывод пусть больших, но конечных сроков окупаемости при явной неэффективности проекта ставит методику под сомнение, т.к. по логике окупаются далеко не все инвестиции. Даже расчет дисконтированных сроков не позволяет ответить на вопрос – при каком уровне процентных ставок срок будет все-таки приемлемым, либо каким должен быть сам доход, чтобы инвестиция окупилась в обозначенные сроки. Осуществление реальных инвестиций на производстве часто предполагает их поэтапное осуществление. При этом, пошаговый расчет кумулятивного дохода может и не достичь очередной отрицательной составляющей потока независимо от того, дисконтированный поток или нет.

Желание повысить точность и учесть разновременность порождает большое количество различных формул и математических подходов к исчислению сроков окупаемости. Отметим здесь, что при дисконтировании показатели времени стоят в степени. Извлечь величину из степени можно только путем логарифмирования. Следовательно, и формула дисконтированного срока окупаемости должна содержать логарифм. Строго говоря, формализована может быть только одна частная ситуация аннуитета.

Аннуитетный поток заслуженно считается особенным, наиболее предпочтительным из всех, т.к. обладает важным свойством сворачиваться по формулам сумм прогрессий.

5.4.3.  Срок окупаемости аннуитетного денежного потока*

Представим, что разовое капиталовложение величиной К генерирует впоследствии равномерный поток доходов на уровне а. Уровень процентных ставок известен. Требуется определить, когда инвестиция окупится, и окупится ли вообще при данном уровне доходов. Поставленная задача иллюстрируется схемой на рис. 21.

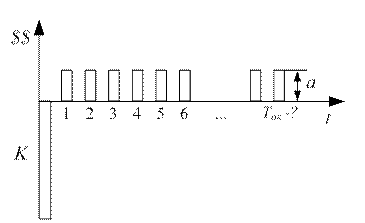
Рис. 21 К расчету срока окупаемости для аннуитетного денежного потока

Такая постановка задачи весьма распространена при реализации реальных инвестиций в производство. Размер взноса аннуитета – разница между увеличением доходов предприятия в каждом периоде времени (ради чего мероприятие и проводилось) и приростом его текущих затрат, если таковое присутствует. Прирост затрат может вызвать повышение размера амортизационных отчислений на новое оборудование, необходимость его технического обслуживания в соответствии с действующими требованиями, потребность в найме либо обучении персонала и т.д.

По определению, за срок окупаемости капитальное вложение К должно быть погашено доходами от него (a) с учетом приведения (дисконтирования). Принимаемую для расчетов процентную ставку обозначим r. Тогда:

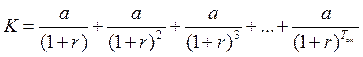                                                          (5.18)

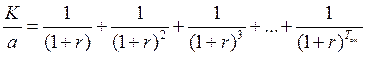
Правая часть выражения – геометрическая прогрессия, такая же, как мы уже рассматривали в разделе 3.3 при расчете настоящей стоимости аннуитетов постнумерандо.

;       ;      ;      .

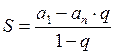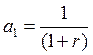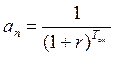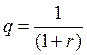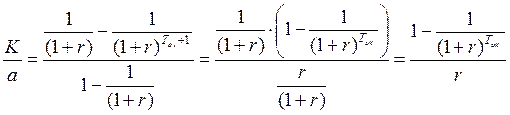
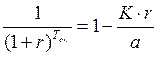
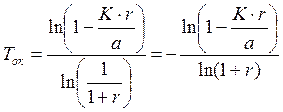                                                                          (5.19)

Знак «минус» в начале формулы не случаен. Выражение  – число, заведомо меньше 1. Поэтому числитель всегда будет отрицательным.

Важное значение имеет и еще один момент. Если  (доли, возмещаемой ежегодно),  будет отрицательно. Логарифм отрицательного числа не существует. Следовательно, не будет существовать и срок окупаемости такого вложения. В этом заключается очень существенное преимущество дисконтированных оценок перед не дисконтированными. Сколь бы значительным не было капитальное вложение, и сколь бы ничтожной не была от него отдача, не дисконтированный Т_ок будет иметь конечное значение. Дисконтированные сроки существуют не всегда, что закономерно, поскольку по логике окупаются далеко не все инвестиции.

Чтобы проиллюстрировать разницу между простым и дисконтированным сроками, приведем пример расчета по данной формуле.

Задача 139*