Экономическая оценка инвестиций: Учебное пособие (Конспект лекций и практикум), страница 36

Пусть капитальное вложение (К) составляет 400 усл. ед. Ежегодная ожидаемая дополнительная прибыль предприятия (а) оценивается в 40 усл. ед. Процентная ставка r=5%. Рассчитать простой и дисконтированный срок окупаемости такой инвестиции. Определить, какой должна быть ежегодная дополнительная прибыль, чтобы дисконтированный срок окупаемости был равен 10 годам.

Простой (не дисконтированный) срок окупаемости составит 10 лет.

Дисконтированный срок

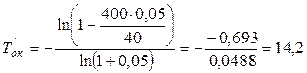 года

При ставке r=7% срок окупаемости составит 17,8 лет, при ставке r=9% – 26,7 лет. Если цена денег превышает 10% (а/K=40/400), данное мероприятие не окупается.

Решаем обратную задачу.

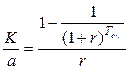
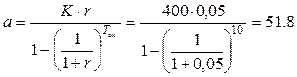 усл. ед.

Задачи, разрешимые для аннуитетных денежных потоков, невозможно столь же просто разрешить, если поток не обладает свойством равномерности. Но, воспользовавшись понятием финансовой эквивалентности, можно приводить неравномерные потоки к эквивалентным аннуитетам.

5.4.4.  Возможные подходы к оценке неординарных денежных потоков*

Денежные потоки считаются неординарными, если выполняется одно из следующих условий:

1. Притоки и оттоки капитала чередуются более одного раза (инвестиции осуществляются этапами);

2. Началу инвестиционного проекта соответствует приток денежных средств, окончанию – отток, либо присутствует один из этих фактов. Такая ситуация на практике встречается довольно часто. Проекты могут стартовать с получения кредитов, предоплат и т.п., а заканчиваться выплатой различных обязательств, выкупом имущества, приобретенного по лизинговым схемам, затратами на возмещение ущерба, нанесенного окружающей среде и т.д.

Такая конфигурация cash flow может свидетельствовать о том, что у проекта будет несколько значений IRR, а срок его окупаемости определится также либо умозрительно, либо в корне не верно. Приведем конкретные примеры.

Табл. 5.5

Примеры неординарных денежных потоков

Первый поток в силу значимости первой положительной суммы не имеет IRR вообще. При его анализе можно выявить, что NPV достигает минимума в 4516 ед. при значении r=109% и далее бесконечно стремится к 5000. Второй поток имеет два значения IRR: 86,2% и 161,6%. Оба потока «окупаются» еще до момента последней выплаты (моменты т.н. «окупаемости» у них возникают несколько раз). При этом, оба потока показывают положительные значения NPV при приемлемых уровнях процентных ставок.

Суть приведения для целей более глубокой оценки сводится к следующему: разделить значение NPV на две составляющие: часть приведенных отрицательных компонент (затрат инвестора) и часть приведенных положительных потоков (его доходов):

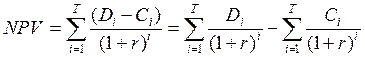                                                         (5.20)

Далее величину приведенных затрат рассматриваем, как единовременную начальную инвестицию, а сумму приведенных доходов – как настоящую стоимость аннуитета постнумерандо продолжительностью Т при ставке r.

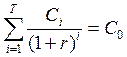                                                                                                         (5.21)

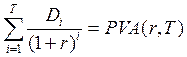                                                                                             (5.22)

Величина единичного дохода тогда может быть определена по формуле:

, где  - стандартная единичная функция для заданных условий (ставки и продолжительности инвестиционного проекта).

Полученный таким образом равномерный поток той же продолжительности будет гарантированно иметь совпадающее значение NPV. Следовательно, выполнится одно из условий возникновения финансовой эквивалентности – равенство результатов. Но из аннуитетного потока всегда можно получить и ставку внутренней доходности, и любые значения сроков окупаемости (простой, дисконтированный, точный).