В момент T кредит полностью амортизируется, т.е. долг становится равным нулю.
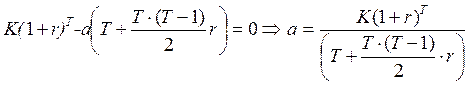 (4.3)
(4.3)
а – размер взноса при известных величине и сроке кредитования.
Формулы 4.2 и 4.3 являются приблизительными и не могут применяться для больших значений T.
Относительная величина взноса ![]() не может быть меньше r, т.к. в этом
случае долг будет копиться, и амортизация не произойдет. Если
не может быть меньше r, т.к. в этом
случае долг будет копиться, и амортизация не произойдет. Если ![]() , сумма долга остается неизменной.
, сумма долга остается неизменной.
Технику приблизительных расчетов можно также использовать как установочную для дальнейшей корректировки на компьютере. Абсолютно точно величина взноса при больших значениях T может быть определена только методом подбора параметра в таблицах Excel.
Задача 120*
Вы заняли на 3 года 15 000 под 8% годовых сложных, начисляемых по схеме сложных процентов, на непогашенный остаток (самоамортизирующийся кредит). Возвращать нужно равными суммами в конце каждого года. Определить размер годового взноса, общую сумму долга, а также общую сумму процентов.
По упрощенной формуле получим:
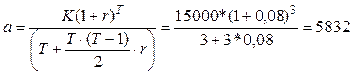
Воспользовавшись формулой точнее (т.к. T не велико), получим:
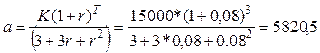
Общая сумма долга ![]() при точном исчислении,
17496 в случае применения упрощенной схемы. Сумма процентов составит,
соответственно, 2461,5 д.е. (2496 при округленных вычислениях).
при точном исчислении,
17496 в случае применения упрощенной схемы. Сумма процентов составит,
соответственно, 2461,5 д.е. (2496 при округленных вычислениях).
Для небольших значений T различия точных и приблизительных величин сводятся к представленным в табл. 4.2. Для длительных сроков кредитования использование упрощенных формул не правомочно, т.к. разница получается весьма существенной. Убедиться в этом наглядно можно на примере задачи №121.
Табл. 4.2
Формулы для расчетов по самоамортизирующимся кредитам при небольших сроках кредитования
|
T |
Точное значение а |
Приблизительное значение, полученное |
|
T=2 |
|
|
|
T=3 |
|
|
|
T=4 |
|
|
|
T=5 |
|
|
|
T=6 |
|
|
Задача 121*
Стоимость квартиры составляет 5 млн. руб. Вам предлагается приобрести ее на условиях ипотечного самоамортизирующегося кредита с первым взносом 10% стоимости. Ставка по ипотечному кредиту – 8% годовых, начисляемых ежемесячно на остаток долга. Долг предполагается погашать равными ежемесячными платежами в течение 30 лет. Определите размер ежемесячного взноса.
Очевидно, что количество периодов в этой задаче равно 360, и разрешить ее можно только с применением компьютера.
По упрощенной формуле получим:
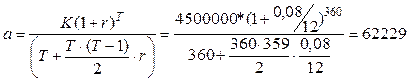
Точное значение величины взноса составляет 33019,4. При ежемесячном взносе в 62229 кредит амортизируется за 99 мес., а не за 360.
Решите эту задачу средствами MS Excel, руководствуясь теорией, а также приведенными ответами для сравнения.
Денежный поток, генерируемый самоамортизирующимся кредитом, обладает одним интересным свойством. Взносы на протяжении выплаты кредита одинаковы по величине, но не одинаковы по своему содержанию. В первые периоды в большей степени отдается процент за кредит, в конечные периоды в большей степени отдается долг (рис. 17). Математически это можно проиллюстрировать следующим образом. Разделим величину постоянного взноса на две части:
![]() , где
, где
![]() - выплата процентов в момент t;
- выплата процентов в момент t;
![]() - выплата основного долга (тела кредита).
- выплата основного долга (тела кредита).
Табл. 4.3
Формулы для расчетов по самоамортизирующимся кредитам при небольших сроках кредитования
|
t |
Сумма процентов за пользование кредитом |
Взнос на погашение основного долга |
Остаток долга |
|
0 |
- |
- |
K |
|
1 |
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
t |
|
|
|
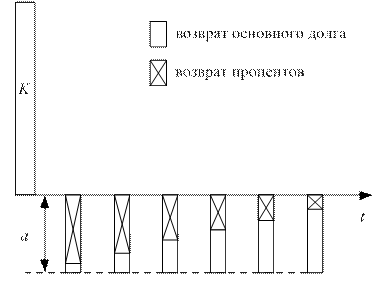
Рис. 17 Структура выплат самоамортизирующегося кредита
Задача 122*
По данным задачи №120 определить, какой процент будет уплачен в третьем году.
Надо разделить взносы на выплату основного долга и проценты.
Проценты за 1-й год составили 15000*0,08=1200
Выплата долга в первом году (5820,5-1200)=4620,5
За второй год проценты составили (15000-4620,5)*0,08=830,36
Уважаемый посетитель!
Чтобы распечатать файл, скачайте его (в формате Word).
Ссылка на скачивание - внизу страницы.