Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 9

Если, например, в уравнении

                                                   (2.17)

функции  и  являются обобщёнными многочленами (или суперпозицией функций от таких многочленов) переменных , то это уравнение при определённых условиях можно свести к однородному подстановкой:

, ,                                                          (2.18)

где ,  - постоянные, отличные от нуля, подобраны так, чтобы после подстановки уравнение

стало однородным. Это возможно тогда, когда функции  и  будут однородными функциями одинакового измерения.

П р и м е р 1. Проинтегрировать уравнение

.

Р е ш е н и е. Замена , . Получаем

.                              (2.19)

Имеем , . Для того, чтобы уравнение (2.19) было однородным, функции  и  должны быть однородными одинакового измерения, то есть должны выполняться равенства:

.

Таким образом, для нахождения  и  решаем систему:

,

где , то есть  можно выбрать произвольное.

Положив , получим  и преобразованное уравнение запишется:

.

Это однородное уравнение, так как 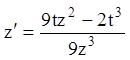 или , так как правая часть последнего уравнения является однородной функцией нулевого измерения. Замена 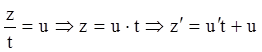. Подставив в уравнение, получаем:

                                                                           ; ; ; .

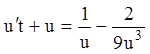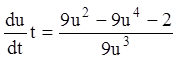Тогда общий интеграл:

.

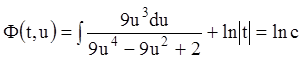Вычисляем интеграл:

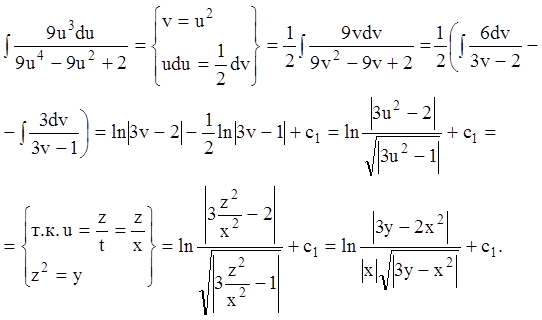
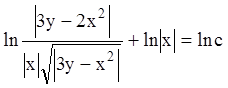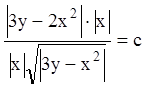Тогда общий интеграл запишется , или , или .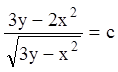

Для сведения уравнения (2.17) к однородному вместо подстановки (2.18) можно использовать также более общую подстановку:

, ,                                         (2.20)

где , , ,  - неизвестные постоянные, которые нужно определить из условия поставленной задачи (полученное после подстановки уравнение должно быть однородным).

В качестве иллюстрации подстановки (2.20) рассмотрим уравнения вида:

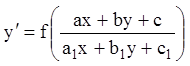,                                            (2.21)

где , , , , ,  - заданные постоянные, а  - непрерывная функция.

Если , то уравнение (2.21) является однородным, так как его правая часть есть функцией от однородной функции нулевого измерения.

Если  (хотя бы одно из чисел ,  отлично от нуля), то сделаем замену (2.20) при . Положим

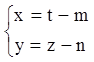                                                           (2.22)

и применим преобразование параллельного переноса начала координат в точку . Подберём координаты ,  этой точки так, чтобы уравнение (2.21) стало однородным. Подставив (2.22) в (2.21), получим уравнение  или

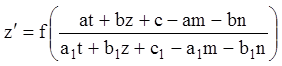.                                  (2.23)

Очевидно, для однородности уравнения необходимо выполнение равенств:

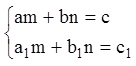,                                         (2.24)

которые представляют собой систему линейных алгебраических уравнений. Если  (), эта система имеет единственное решение. Решив систему (2.24) и однородное уравнение (2.23), получим, согласно (2.22), общий интеграл уравнения (2.21).

Если же , то 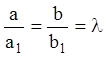, то предложенный выше метод неприменим, но в этом случае подстановка  сразу превращает уравнение (2.21) в уравнение с разделяющимися переменными: так как 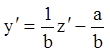, то ; .

ЛЕКЦИЯ №3.

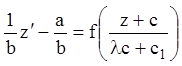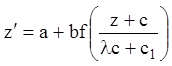Тема: 3. Линейные дифференциальные уравнения и к ним сводящиеся.

ПЛАН

3.1 Методы решения линейных дифференциальных уравнений первого порядка

3.1.1 Метод Бернулли

3.1.2 Метод вариации произвольных постоянных (метод Лагранжа)

3.1.3 Метод Эйлера

3.2 Свойства линейного уравнения и его решений

3.3 Уравнения, сводящиеся к линейным

3.1 Методы решения линейных дифференциальных уравнений первого порядка

Дифференциальное уравнение 1-го порядка называют линейным, если искомая функция и её производная входят в уравнение в первой степени (т. е. линейно) и не перемножаются. По этому определению линейное уравнение можно записать в виде:

.                                                (3.1)

где ,  - заданные непрерывные в рассматриваемой области функции.

При  уравнение (3.1) называют линейным однородным уравнением первого порядка:

.                                                      (3.2)

В связи с этим уравнение (3.1) при  называют линейным неоднородным уравнением.