Дифференциальные уравнения и математическое моделирование. Основные понятия дифференциальных уравнений. Метод Изоклин, страница 19

Если уравнения  интегрировались в явном виде лишь в простейших случаях, то дифференциальные уравнения вида (5.7) интегрируются еще реже. Поэтому часто приходится решения таких уравнений представлять в неявном , и даже в параметрическом виде

, .

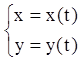Предположим, что уравнение (5.7) в каждой точке M(x,y) некоторой области определяет одно или несколько значений y' . Тогда, построив в каждой точке M(x,y) этой области единичные отрезки, наклон которых к оси OX определяется соответствующим значением y', получим некоторое поле направлений. Следовательно, с геометрической точки зрения (как и для уравнения  ) интегрирование уравнения (5.7) сводится к отысканию среди возможных кривых такой кривой, касательная к которой в каждой ее точке имела бы направление, совпадающее с направлением поля, заданного дифференциальным уравнением в этой точке.

П р и м е р 1. Решить уравнение:

Р е ш е н и е. Разрешая это уравнение как квадратное относительно y', получаем:  .

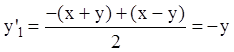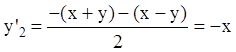;    , т.е.

,     .

Интегрируя каждое из полученных уравнений, находим:

, ,  ,  ,

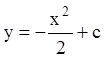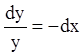где с – произвольная постоянная.

Следовательно, через каждую точку M(x,y) плоскости XOY проходят две интегральные кривые.

Задача Коши для уравнения (5.7) ставится обычным образом: найти решение уравнения (5.7), которое при  принимает значение . Геометрически она интерпретируется также: среди множества интегральных кривых уравнения (5.7) выделить одну, проходящую через заданную точку M₀(x₀,y₀).

Предположим, что уравнение (5.7) может быть разрешенным относительно производной. Тогда в некоторой окрестности точки M₀(x₀,y₀) получим для y' в общем случае несколько вещественных значений:

                    (5.8)

При этом, если каждая из функций удовлетворяет теореме существования и единственности решения, то через эту точку M₀(x₀,y₀) будет проходить m интегральных кривых уравнения (5.7). Если при этом каждая интегральная кривая имеет наклон касательной, не совпадающий с наклоном касательной других интегральных кривых, то говорят, что задача Коши имеет единственное решение.

Введем понятие общего интеграла, частного и особого решения уравнения (5.7).

С этой целью предположим, что уравнение (5.7) в окрестности точки M₀(x₀,y₀) может быть разрешено относительно y', т.е. распадается на уравнения (5.8). И пусть каждое из этих уравнений имеет общее решение:

                                                 (5.9)

или общий интеграл

,                                      (5.10)

где с – произвольная постоянная.

Тогда совокупность общих решений (5.9) или совокупность общих интегралов (5.10) будем называть общим интегралом уравнения (5.7).

П р и м е р 2. Найти общий интеграл уравнения:

Р е ш е н и е. Разрешив это уравнение относительно y', получим три дифференциальных уравнения:

.

Решив их, получим общие решения:

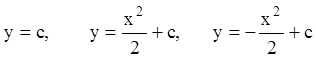                                      (5.11)

Совокупность общих решений и есть общий интеграл исходного дифференциального уравнения, который, как это видно из рис.15, представляет наложение семейств интегральных кривых (5.11).

Заметим, что решение задачи Коши для рассмотренного примера в каждой точке плоскости XOY, не лежащей на оси OY, единственно (угловые коэффициенты касательных различны  ).

В точках, лежащих на оси OY, направление полей совпадает.

Решение  уравнения (5.7) называется частным решением этого уравнения, если в каждой его точке задача Коши имеет единственное решение.

Особым решением уравнения (5.7) называют решение, которое во всех своих точках не обладает свойством единственности, т.е. через каждую точку этого решения проходит не менее двух интегральных кривых, имеющих одинаковое направление  касательной.

Заметим, что в приведенном примере ось OY (x=o) не является интегральной кривой этого уравнения, а во всех остальных точках плоскости XOY задача Коши этого уравнения имеет единственное решение. Таким образом, решенное уравнение не имеет особых решений.

5.3 Типы дифференциальных уравнений, не разрешенных относительно производной

Рассмотрим частные типы дифференциальных уравнений вида (5.7), для которых можно указать способы нахождения решений.